Bài tập 3.36 trang 130 SBT Hình học 12

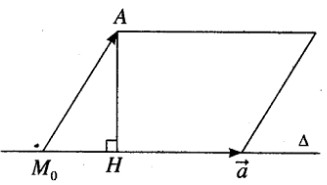
Đường thẳng \(\Delta \) đi qua điểm M₀(1; 0; 0) và có vecto chỉ phương \(\vec a = (2;2;1)\).

Ta có \(\overrightarrow {{M_0}A}  = (0;0;1),\vec n = \vec a \wedge \overrightarrow {{M_0}A}  = (2; - 2;0)\)

\(d(A,{\rm{\Delta }}) = \frac{{|\vec n|}}{{|\vec a|}} = \frac{{\sqrt {4 + 4 + 0} }}{{\sqrt {4 + 4 + 1} }} = \frac{{2\sqrt 2 }}{3}\)

Vậy khoảng cách từ điểm A đến \(\Delta \) là \(\frac{{2\sqrt 2 }}{3}\).

-- Mod Toán 12 HỌC247