Giải bài 3.43 tr 131 SBT Hình học 12
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Bằng phương pháp tọa độ hãy tính khoảng cách giữa hai đường thẳng CA’ và DD’.
Hướng dẫn giải chi tiết
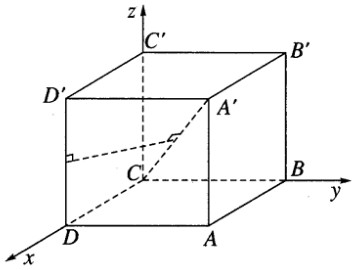
Ta chọn hệ trục tọa độ sao cho: C là gốc tọa độ, \(\overrightarrow {CD} = a\vec i;\overrightarrow {CB} = a\vec j;\overrightarrow {CC'} = a\vec k\)
Trong hệ tọa độ vừa chọn ta có: C(0; 0; 0), A’(a; a ; a), D(a,; 0;0), D’(a; 0; a)
\(\overrightarrow {CA'} = (a;a;a),\overrightarrow {{\rm{D}}{{\rm{D}}^\prime }} = (0;0;a)\)
Gọi \((\alpha )\) là mặt phẳng chứa \(\overrightarrow {CA'}\) và song song với \(\overrightarrow {DD'}\). Mặt phẳng \((\alpha )\) có vecto pháp tuyến là: \(\vec n = \overrightarrow {CA'} \wedge \overrightarrow {D{D^\prime }} = ({a^2}; - {a^2};0)\) hay x – y = 0
Phương trình tổng quát của \((\alpha )\) là x – y = 0.
Ta có: \(d(CA',{\rm{D}}{{\rm{D}}^\prime }) = d(D,(\alpha )) = \frac{{| - a|}}{{\sqrt {1 + 1 + 0} }} = \frac{a}{{\sqrt 2 }}\)
Vậy khoảng cách giữa hai đường thẳng CA’ và DD’ là \(\frac{{a\sqrt 2 }}{2}\).
-- Mod Toán 12 HỌC247
-


Viết phương trình đường thẳng d qua trọng tâm G của tam giác OAB biết A(1;4;2), B(-1;2;4)
bởi Thảo Phương
 19/02/2020
19/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Viết phương trình mặt phẳng p qua M (1;2;1) lần lượt cắt các tia Ox, Oy, Oz tại điểm A, B, C sao cho hình chóp O.ABC đều
bởi Đinh Phát
 17/02/2020
viết phương trình mặt phẳng p qua M (1;2;1) lần lượt cắt các tia Ox Oy Oz tại điểm A, B, C sao cho hình chóp O.ABC đềuTheo dõi (0) 0 Trả lời
17/02/2020
viết phương trình mặt phẳng p qua M (1;2;1) lần lượt cắt các tia Ox Oy Oz tại điểm A, B, C sao cho hình chóp O.ABC đềuTheo dõi (0) 0 Trả lời -

 Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:x−1/1=y−2/2=z 2/−2. Tính khoảng cách d từ điểm M(-2;1;-1) tới dTheo dõi (0) 0 Trả lời
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:x−1/1=y−2/2=z 2/−2. Tính khoảng cách d từ điểm M(-2;1;-1) tới dTheo dõi (0) 0 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính góc O của tam giác OAB biết A(2;0;2), B(0;2;2)
bởi Trần Phillip
 13/02/2020
Trong không gian với hệ trục tọa độOxyz, cho A 2;0; 2 , B0; 2; 2 . Góc Ocủa tam giác OABbằngTheo dõi (0) 2 Trả lời
13/02/2020
Trong không gian với hệ trục tọa độOxyz, cho A 2;0; 2 , B0; 2; 2 . Góc Ocủa tam giác OABbằngTheo dõi (0) 2 Trả lời -


Tính khoảng cách d từ I đến mặt phẳng (P) biết mặt cầu S(I;R) có bán kính R=3
bởi Nguyễn Thanh Tân
 11/02/2020
Giúp mình vớiTheo dõi (0) 1 Trả lời
11/02/2020
Giúp mình vớiTheo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 3.40 trang 130 SBT Hình học 12
Bài tập 3.42 trang 131 SBT Hình học 12
Bài tập 3.44 trang 131 SBT Hình học 12
Bài tập 3.45 trang 131 SBT Hình học 12
Bài tập 24 trang 102 SGK Hình học 12 NC
Bài tập 25 trang 102 SGK Hình học 12 NC
Bài tập 26 trang 102 SGK Hình học 12 NC
Bài tập 27 trang 103 SGK Hình học 12 NC
Bài tập 28 trang 103 SGK Hình học 12 NC
Bài tập 29 trang 103 SGK Hình học 12 NC
Bài tập 30 trang 103 SGK Hình học 12 NC
Bài tập 31 trang 103 SGK Hình học 12 NC
Bài tập 32 trang 104 SGK Hình học 12 NC
Bài tập 33 trang 104 SGK Hình học 12 NC





