Bài tập 24 trang 102 SGK Hình học 12 NC
Viết phương trình tham số và chính tắc (nếu có) của các đường thẳng sau đây:
a) Các trục tọa độ Ox, Oy, Oz.
b) Các đường thẳng đi qua điểm M0(x0; y0 ; z0) (với \({x_0}.{y_0}.{z_0} \ne 0\) và song song với mỗi trục tọa độ;
c) Đường thẳng đi qua M(2; 0; −1) và có vectơ chỉ phương \(\overrightarrow u = ( - 1;3;5)\)
d) Đường thẳng đi qua N(−2; 1; 2) và có vectơ chỉ phương \(\overrightarrow u = ( 0; 0; -3)\)
e) Đường thẳng đi qua N(3; 2; 1) và vuông góc với mặt phẳng 2x − 5y + 4 = 0
g) Đường thẳng đi qua P(2; 3; −1) và Q(1; 2; 4)
Hướng dẫn giải chi tiết
a) Trục Ox đi qua O(0; 0; 0) và có vectơ chỉ phương \(\overrightarrow i = (1;0;0)\) nên có phương trình tham số là
\(\left\{ \begin{array}{l}
x = t\\
y = 0\\
z = 0
\end{array} \right.\)
Tương tự, trục Oy có phương trình tham số là
\(\left\{ \begin{array}{l}
x = 0\\
y = t\\
z = 0
\end{array} \right.\)
Tương tự, trục Oz có phương trình tham số là
\(\left\{ \begin{array}{l}
x = 0\\
y = 0\\
z = t
\end{array} \right.\)
Các phương trình đó không có phương trình chính tắc.
b) Đường thẳng đi qua M0(x0; y0; z0) song song với trục Ox có vectơ chỉ phương \(\overrightarrow i = (1;0;0)\) nên có phương trình tham số là
\(\begin{array}{l}
\overrightarrow i = (1;0;0)\\
\left\{ \begin{array}{l}
x = {x_0} + t\\
y = {y_0}\\
z = {z_0}
\end{array} \right.
\end{array}\)
Tương tự đường thẳng đi qua M0 với trục Oy có phương trình tham số là
\(\begin{array}{l}
\overrightarrow i = (1;0;0)\\
\left\{ \begin{array}{l}
x = {x_0} \\
y = {y_0}+t\\
z = {z_0}
\end{array} \right.
\end{array}\)
Đường thẳng đi qua M0 với trục Oz có phương trình tham số là
\(\begin{array}{l}
\overrightarrow i = (1;0;0)\\
\left\{ \begin{array}{l}
x = {x_0} \\
y = {y_0}\\
z = {z_0} + t
\end{array} \right.
\end{array}\)
c) Đường thẳng đi qua M(2; 0; −1) có vectơ chỉ phương có phương trình tham số: \(\vec u = \left( { - 1;3;5} \right)\) Tương tự đường thẳng đi qua M0 với trục Oy có phương trình tham số là
\(\left\{ \begin{array}{l}
x = 2 - t\\
y = 3t\\
z = - 1 + 5t
\end{array} \right.\)
Và có phương trình chính tắc:
\(\frac{{x - 2}}{{ - 1}} = \frac{y}{3} = \frac{{z + 1}}{5}\)
d) Đường thẳng đi qua N(−2; 1; 2) và có vectơ chỉ phương \(\vec u = \left( {0;0; - 3} \right)\) có phương trình tham số
\(\left\{ \begin{array}{l}
x = - 2\\
y = 1\\
z = 2 - 3t
\end{array} \right.\)
⇒ Không có phương trình chính tắc
e) Vectơ chỉ phương \(\overrightarrow u \) của đường thẳng là vectơ pháp tuyến của mặt phẳng 2x − 5y + 4 = 0 nên \(\overrightarrow u = \left( {2; - 5;0} \right)\).
Vậy đường thẳng có phương trình tham số\
\(\left\{ \begin{array}{l}
x = 3 + 2t\\
y = 2 - 5t\\
z = 1
\end{array} \right.\)
Không có phương trình chính tắc
g) Đường thẳng đi qua P(2; 3; −1) có vectơ chỉ phương \(\overrightarrow {PQ} = \left( { - 1; - 1;5} \right)\) nên có phương trình tham số là
\(\left\{ \begin{array}{l}
x = 2 - t\\
y = 3 - t\\
z = - 1 + 5t
\end{array} \right.\)
Phương trình chính tắc :
\(\frac{{x - 2}}{{ - 1}} = \frac{{y - 3}}{{ - 1}} = \frac{{z + 1}}{5}\)
-- Mod Toán 12 HỌC247
-

 cho ba điểm A((2,0,1) B(1,0,0) C(1,1,1) và mặt phẳng P :x y z-2=0. điểm M(a,b,c) nằm trên P thoả mãn MA=MB=MC. T=a 2b cTheo dõi (0) 0 Trả lời
cho ba điểm A((2,0,1) B(1,0,0) C(1,1,1) và mặt phẳng P :x y z-2=0. điểm M(a,b,c) nằm trên P thoả mãn MA=MB=MC. T=a 2b cTheo dõi (0) 0 Trả lời -


Viết phương trình đường thẳng d song song với (P) cắt đường thẳng a, b tại M, N sao cho MN=căn 2
bởi Anh Phạm Thị Lan
 08/01/2020
08/01/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


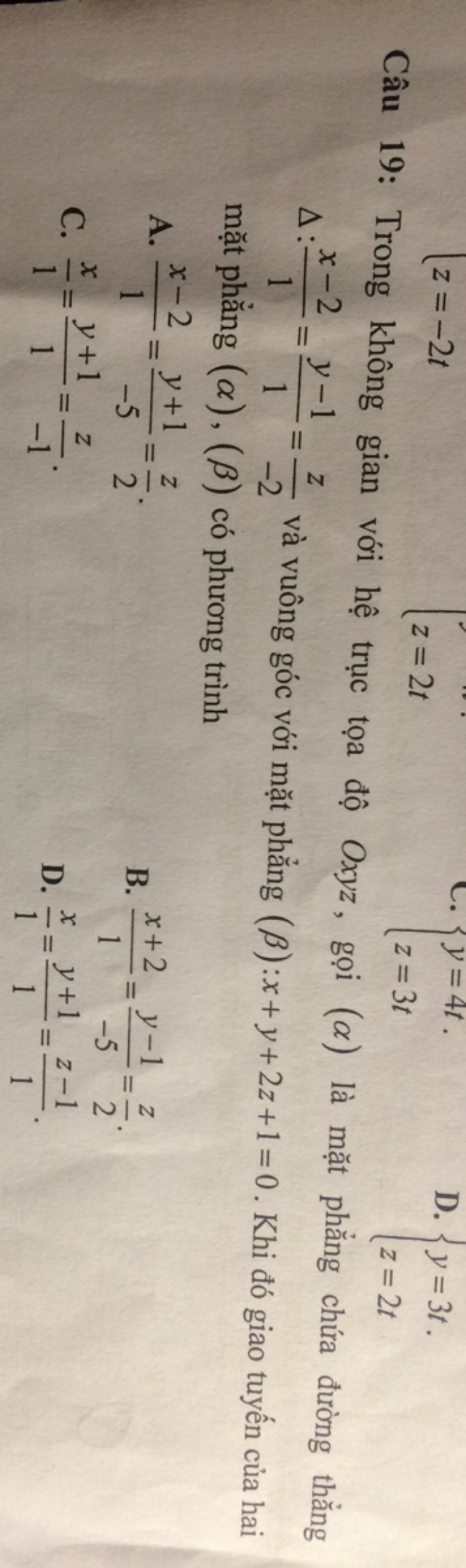 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Lập phương trình đường thẳng d biết d là giao tuyến của hai mặt phẳng
bởi Nguyễn Hoàng Long
 07/01/2020
Lập ptđt d biết d là giao tuyến của 2 mặt phẳngTheo dõi (0) 0 Trả lời
07/01/2020
Lập ptđt d biết d là giao tuyến của 2 mặt phẳngTheo dõi (0) 0 Trả lời -


Tìm vecto pháp tuyến của mặt phẳng (p) biết mặt phẳng (p) có phưong trình 3x-z+1=0
bởi Nguyễn Ben
 27/12/2019
27/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chỉ ra một vecto không phải là vecto chỉ phương của đường thẳng đã cho?
bởi Nguyễn Khánh Vy
 04/12/2019
Đáp án A. (-2;3;-3) B. (4;-6;6) C. (1;2;-1) D. (2;-3;3Theo dõi (0) 0 Trả lời
04/12/2019
Đáp án A. (-2;3;-3) B. (4;-6;6) C. (1;2;-1) D. (2;-3;3Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 3.44 trang 131 SBT Hình học 12
Bài tập 3.45 trang 131 SBT Hình học 12
Bài tập 25 trang 102 SGK Hình học 12 NC
Bài tập 26 trang 102 SGK Hình học 12 NC
Bài tập 27 trang 103 SGK Hình học 12 NC
Bài tập 28 trang 103 SGK Hình học 12 NC
Bài tập 29 trang 103 SGK Hình học 12 NC
Bài tập 30 trang 103 SGK Hình học 12 NC
Bài tập 31 trang 103 SGK Hình học 12 NC
Bài tập 32 trang 104 SGK Hình học 12 NC
Bài tập 33 trang 104 SGK Hình học 12 NC





