Phß║¦n hŲ░ß╗øng dß║½n giß║Żi b├Āi tß║Łp SGK b├Āi 3 ─Éß║Īo h├Ām cß╗¦a h├Ām sß╗æ lŲ░ß╗Żng gi├Īc sß║Į gi├║p c├Īc em nß║»m ─æŲ░ß╗Żc phŲ░ŲĪng ph├Īp v├Ā r├©n luyß╗ćn k─® n─āng t├Łnh ─æß║Īo h├Ām cß╗¦a c├Īc h├Ām sß╗æ lŲ░ß╗Żng gi├Īc tß╗½ SGK ─Éß║Īi sß╗æ v├Ā Giß║Żi t├Łch 11 CŲĪ bß║Żn v├Ā N├óng cao.
-
B├Āi tß║Łp 1 trang 168 SGK ─Éß║Īi sß╗æ & Giß║Żi t├Łch 11
T├¼m ─æß║Īo h├Ām cß╗¦a c├Īc h├Ām sß╗æ sau:
a) \(y = \frac{x-1}{5x-2}\);
b) \(y =\frac{2x+3}{7-3x}\);
c) \(y =\frac{x^{2}+2x+3}{3-4x}\);
d) \(y =\frac{x^{2}+7x+3}{x^{2}-3x}\).
-
B├Āi tß║Łp 2 trang 168 SGK ─Éß║Īi sß╗æ & Giß║Żi t├Łch 11
Giß║Żi c├Īc bß║źt phŲ░ŲĪng tr├¼nh sau:
a) \(y'<0\) vß╗øi \(y = \frac{x^{2}+x+2}{x-1}\) ;
b) \(y'\geq 0\) vß╗øi \(y =\frac{x^{2}+3}{x+1}\);
c) \(y'>0\) vß╗øi \(y =\frac{2x-1}{x^{2}+x+4}\).
-
B├Āi tß║Łp 3 trang 169 SGK ─Éß║Īi sß╗æ & Giß║Żi t├Łch 11
T├¼m ─æß║Īo h├Ām cß╗¦a c├Īc h├Ām sß╗æ sau:
a) \(y = 5sinx -3cosx\)
b) \(y=\frac{sinx+cosx}{sinx-cosx}\)
c) \(y = x cotx\)
d) \(y =\frac{sinx}{x}\) + \(\frac{x}{{\sin x}}\)
e) \(y = \sqrt{(1 +2tan x)}\)
f) \(y = sin\sqrt{(1 +x^2}).\)
-
B├Āi tß║Łp 4 trang 169 SGK ─Éß║Īi sß╗æ & Giß║Żi t├Łch 11
T├¼m ─æß║Īo h├Ām cß╗¦a c├Īc h├Ām sß╗æ sau:
a) \(y = (9 -2x)(2x^3- 9x^2 +1)\);
b) \(y=\left ( 6\sqrt{x} -\frac{1}{x^{2}}\right )(7x -3)\) ;
c) \(y = (x -2)\sqrt{(x^2 +1)}\);
d) \(y = tan^2x +cotx^2\);
e) \(y = cos \frac{x}{1+x}\).
-
B├Āi tß║Łp 5 trang 169 SGK ─Éß║Īi sß╗æ & Giß║Żi t├Łch 11
T├Łnh \(\frac{{f'(x)}}{{\varphi (1)'}}\), biß║┐t rß║▒ng \(f(x) = x^2\) v├Ā \(\varphi (x) = 4x +sin\)\(\frac{{\pi x}}{2}\).
-
B├Āi tß║Łp 6 trang 169 SGK ─Éß║Īi sß╗æ & Giß║Żi t├Łch 11
Chß╗®ng minh rß║▒ng c├Īc h├Ām sß╗æ sau c├│ ─æß║Īo h├Ām kh├┤ng phß╗ź thuß╗Öc x:
a) \(sin^6x + cos^6x + 3sin^2x.cos^2x\);
b) \(cos^2\)\(\left( {\frac{\pi }{3} - x} \right)\) \(+\) \(cos^2\)\(\left( {\frac{\pi }{3} + x} \right)\) \(+\) \(cos^2\)\(\left( {\frac{2\pi }{3} - x} \right)\) \(+\) \(cos^2\) \(\left( {\frac{2\pi }{3} + x} \right)\) \(-2sin^2x\).
-
B├Āi tß║Łp 7 trang 169 SGK ─Éß║Īi sß╗æ & Giß║Żi t├Łch 11
Giß║Żi phŲ░ŲĪng tr├¼nh \(f'(x) = 0\), biß║┐t rß║▒ng:
a) \(f(x) = 3cosx + 4sinx + 5x\);
b) \(f(x) = 1 - sin(\pi + x) + 2cos \left ( \frac{2\pi +x}{2} \right )\).
-
B├Āi tß║Łp 8 trang 169 SGK ─Éß║Īi sß╗æ & Giß║Żi t├Łch 11
Giß║Żi bß║źt phŲ░ŲĪng tr├¼nh \(f'(x) > g'(x)\), biß║┐t rß║▒ng:
a) \(f(x) = x^3 + x - \sqrt{2}, g(x) = 3x^2 + x + \sqrt{2}\) ;
b) \(f(x) = 2x^3 - x^2 + \sqrt{3}, g(x) = x^3 +\frac{x^{2}}{2}-\sqrt{3}\).
-
B├Āi tß║Łp 5.40 trang 207 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \sqrt {{{\tan }^3}x} \)
-
B├Āi tß║Łp 5.41 trang 207 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \frac{2}{{\cos \left( {\frac{\pi }{6} - 5x} \right)}}\)
-
B├Āi tß║Łp 5.42 trang 207 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \sqrt x + \frac{1}{{\sqrt x }} + 0,1{x^{10}}\)
-
B├Āi tß║Łp 5.43 trang 207 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \frac{{2{x^2} + x + 1}}{{{x^2} - x + 1}}\)
-
B├Āi tß║Łp 5.44 trang 207 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(g\left( \varphi \right) = \frac{{\cos \varphi + \sin \varphi }}{{1 - \cos \varphi }}\)
-
B├Āi tß║Łp 5.45 trang 207 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = {\left( {1 + 3x + 5{x^2}} \right)^4}\)
-
B├Āi tß║Łp 5.46 trang 207 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = {\sin ^2}3x + \frac{1}{{{{\cos }^2}x}}\)
-
B├Āi tß║Łp 5.47 trang 207 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \sqrt {x + \sqrt {x + \sqrt x } } \)
-
B├Āi tß║Łp 5.48 trang 208 SBT To├Īn 11
Giß║Żi phŲ░ŲĪng tr├¼nh \(f'\left( x \right) = 0\), biß║┐t rß║▒ng:
a) \({f\left( x \right) = 3x + \frac{{60}}{x} - \frac{{64}}{{{x^3}}} + 5}\)
b) \({f\left( x \right) = \frac{{\sin 3x}}{3} + \cos x - \sqrt 3 \left( {\sin x + \frac{{\cos 3x}}{3}} \right)}\)
-
B├Āi tß║Łp 5.49 trang 208 SBT To├Īn 11
Giß║Żi c├Īc phŲ░ŲĪng tr├¼nh:
a) \(f'\left( x \right) = 0\) vß╗øi \(f\left( x \right) = 1 - \sin \left( {\pi + x} \right) + 2\cos \left( {\frac{{3\pi + x}}{2}} \right)\)
b) \(g'\left( x \right) = 0\) vß╗øi \(g\left( x \right) = \sin 3x - \sqrt 3 \cos 3x + 3\left( {\cos x - \sqrt 3 \sin x} \right)\)
-
B├Āi tß║Łp 5.50 trang 208 SBT To├Īn 11
Giß║Żi phŲ░ŲĪng tr├¼nh \(f'\left( x \right) = g'\left( x \right)\)
a) Vß╗øi \(f\left( x \right) = 1 - {\sin ^4}3x\) v├Ā \(g\left( x \right) = \sin 6x\)
b) Vß╗øi \(f\left( x \right) = 4x{\cos ^2}\left( {\frac{x}{2}} \right)\) v├Ā \(g\left( x \right) = 8\cos \frac{x}{2} - 3 - 2x\sin x\)
-
B├Āi tß║Łp 5.51 trang 208 SBT To├Īn 11
Chß╗®ng minh rß║▒ng \(f'(x) = 0,\forall x \in R\), nß║┐u:
-
B├Āi tß║Łp 5.52 trang 208 SBT To├Īn 11
Tìm \(f'\left( 1 \right),f'\left( 2 \right),f'\left( 3 \right)\) nếu \(f\left( x \right) = \left( {x - 1} \right){\left( {x - 2} \right)^2}{\left( {x - 3} \right)^3}\)
-
B├Āi tß║Łp 5.53 trang 208 SBT To├Īn 11
Tìm \(f'\left( 2 \right)\) nếu \(f\left( x \right) = {x^2}\sin \left( {x - 2} \right)\)
-
B├Āi tß║Łp 5.54 trang 208 SBT To├Īn 11
Cho \(y = \frac{{{x^3}}}{3} + \frac{{{x^2}}}{2} - 2x\)
Vß╗øi gi├Ī trß╗ŗ n├Āo cß╗¦a th├¼:
a) \(y'\left( x \right) = 0\)
b) \(y'\left( x \right) = - 2\);
c)
-
B├Āi tß║Łp 5.55 trang 208 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = {a^5} + 5{a^3}{x^2} - {x^5}\)
-
B├Āi tß║Łp 5.56 trang 208 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \left( {x - a} \right)\left( {x - b} \right)\)
-
B├Āi tß║Łp 5.57 trang 208 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \frac{{ax + b}}{{a + b}}\)
-
B├Āi tß║Łp 5.58 trang 208 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \left( {x + 1} \right){\left( {x + 2} \right)^2}{\left( {x + 3} \right)^3}\)
-
B├Āi tß║Łp 5.59 trang 208 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \left( {x\sin \alpha + \cos \alpha } \right)\left( {x\cos \alpha - \sin \alpha } \right)\)
-
B├Āi tß║Łp 5.60 trang 208 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \left( {1 + n{x^m}} \right)\left( {1 + m{x^n}} \right)\)
-
B├Āi tß║Łp 5.61 trang 209 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \left( {1 - x} \right){\left( {1 - {x^2}} \right)^2}{\left( {1 - {x^3}} \right)^3}\)
-
B├Āi tß║Łp 5.62 trang 209 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \frac{{1 + x - {x^2}}}{{1 - x + {x^2}}}\)
-
B├Āi tß║Łp 5.63 trang 209 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \frac{x}{{{{\left( {1 - x} \right)}^2}{{\left( {1 + x} \right)}^3}}}\)
-
B├Āi tß║Łp 5.64 trang 209 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \frac{{\left( {2 - {x^2}} \right)\left( {3 - {x^3}} \right)}}{{{{\left( {1 - x} \right)}^2}}}\)
-
B├Āi tß║Łp 5.65 trang 209 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = x\sqrt {1 + {x^2}} \)
-
B├Āi tß║Łp 5.66 trang 209 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \frac{x}{{\sqrt {{a^2} - {x^2}} }}\)
-
B├Āi tß║Łp 5.67 trang 209 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \sin \left( {{{\cos }^2}x} \right).\cos \left( {{{\sin }^2}x} \right)\)
-
B├Āi tß║Łp 5.68 trang 209 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \frac{{\sin x - x\cos x}}{{\cos x + x\sin x}}\)
-
B├Āi tß║Łp 5.69 trang 209 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \tan x - \frac{1}{3}{\tan ^3}x + \frac{1}{5}{\tan ^5}x\)
-
B├Āi tß║Łp 5.70 trang 209 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \frac{{\sin {x^2}}}{x}\)
-
B├Āi tß║Łp 5.71 trang 209 SBT To├Īn 11
Cho h├Ām sß╗æ \({y = \cos \frac{x}{{x + 1}}}\). T├¼m
-
B├Āi tß║Łp 5.72 trang 209 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = {\tan ^2}x - \cot {x^2}\)
-
B├Āi tß║Łp 5.73 trang 209 SBT To├Īn 11
Cho \(f\left( t \right) = \frac{{\cos t}}{{1 - \sin t}}\). T├Łnh \(f'\left( {\frac{\pi }{6}} \right)\)
A. -2
B. -3
C. 2
D. 5
-
B├Āi tß║Łp 5.74 trang 210 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = {\left( {3 - \sin x} \right)^3}\)
-
B├Āi tß║Łp 5.75 trang 210 SBT To├Īn 11
Cho \(f\left( x \right) = \sqrt {1 - 2\tan x} \) T├Łnh \(f'\left( {\frac{\pi }{4}} \right)\)
-
B├Āi tß║Łp 5.76 trang 210 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a \(g\left( \varphi \right) = \frac{{\cos \varphi + \sin \varphi }}{{1 - \cos \varphi }}\)
-
B├Āi tß║Łp 5.77 trang 210 SBT To├Īn 11
Cho h├Ām sß╗æ \(y = \cot \sqrt {1 + {x^2}} \). T├Łnh
-
B├Āi tß║Łp 5.78 trang 210 SBT To├Īn 11
Cho \(f\left( x \right) = 5{x^2} - 16\sqrt x + 7\). T├Łnh \(f'\left( 4 \right);f'\left( {\frac{1}{4}} \right)\)
-
B├Āi tß║Łp 5.79 trang 210 SBT To├Īn 11
Cho \(g\left( x \right) = {x^2}\sin \left( {x - 2} \right)\). T├Łnh
A. -2 B. 4 C. 2 D. 1 -
B├Āi tß║Łp 5.80 trang 211 SBT To├Īn 11
T├¼m ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y = \tan \frac{x}{2} - \cot \frac{x}{2}\)
-
B├Āi tß║Łp 5.81 trang 211 SBT To├Īn 11
Giß║Żi phŲ░ŲĪng tr├¼nh \(f'\left( x \right) = g\left( x \right)\) biß║┐t
\(g\left( x \right) = \sin x\) v├Ā \(f\left( x \right) = \left( {2 - {x^2}} \right)\cos x + 2x\sin x\)
-
B├Āi tß║Łp 28 trang 211 SGK To├Īn 11 NC
T├¼m c├Īc giß╗øi hß║Īn sau:
\(\begin{array}{l}
a)\mathop {lim}\limits_{x \to 0} \frac{{tan2x}}{{sin5x}}\\
b)\mathop {lim}\limits_{x \to 0} \frac{{1 - cos2x}}{{xsin2x}}\\
c)\mathop {lim}\limits_{x \to 0} \frac{{1 + sinx - cosx}}{{1 - sinx - cosx}}
\end{array}\) -
B├Āi tß║Łp 29 trang 211 SGK To├Īn 11 NC
T├¼m ─æß║Īo h├Ām cß╗¦a c├Īc h├Ām sß╗æ sau :
\(\begin{array}{*{20}{l}}
{a)y = 5\sin x - 3\cos x}\\
{b)y = \sin ({x^2} - 3x + 2)}\\
{c)y = \cos \sqrt {2x + 1} }\\
{d)y = 2\sin 3x\cos 5x}\\
{e)y = \frac{{\sin x + \cos x}}{{\sin x - \cos x}}}\\
{f)y = \sqrt {\cos 2x} }
\end{array}\) -
B├Āi tß║Łp 30 trang 211 SGK To├Īn 11 NC
Chß╗®ng minh rß║▒ng h├Ām sß╗æ \(y = si{n^6}x + co{s^6}x + 3si{n^2}xco{s^2}x\) c├│ ─æß║Īo h├Ām bß║▒ng 0.
-
B├Āi tß║Łp 31 trang 212 SGK To├Īn 11 NC
T├¼m ─æß║Īo h├Ām cß╗¦a c├Īc h├Ām sß╗æ sau :
\(\begin{array}{*{20}{l}}
{a)y = \tan \frac{{x + 1}}{2}}\\
{b)y = \cot \sqrt {{x^2} + 1} }\\
{c)y = {{\tan }^3}x + \cot 2x}\\
{d)y = \tan 3x - \cot 3x}\\
{e)y = \sqrt {1 + 2\tan x} }\\
{f)y = x\cot x}
\end{array}\) -
B├Āi tß║Łp 32 trang 212 SGK To├Īn 11 NC
Chß╗®ng minh rß║▒ng :
a. H├Ām sß╗æ y = tanx thß╗Åa m├Żn hß╗ć thß╗®c yŌĆ▓ ŌłÆ y2 ŌłÆ 1 = 0
b. H├Ām sß╗æ y = cot2x thß╗Åa m├Żn hß╗ć thß╗®c yŌĆ▓ + 2y2 + 2 = 0
-
B├Āi tß║Łp 33 trang 212 SGK To├Īn 11 NC
T├¼m ─æß║Īo h├Ām cß╗¦a mß╗Śi h├Ām sß╗æ sau :
\(\begin{array}{*{20}{l}}
{a)y = \frac{{\sin x}}{x} + \frac{x}{{\sin x}}}\\
{b)y = \frac{{{{\sin }^2}x}}{{1 + \tan 2x}}}\\
{c)y = \tan (\sin x)}\\
{d)y = x\cot ({x^2} - 1)}\\
{e)y = {{\cos }^2}\sqrt {\frac{\pi }{4} - 2x} }\\
{f)y = x\sqrt {\sin 3x} }
\end{array}\) -
B├Āi tß║Łp 34 trang 212 SGK To├Īn 11 NC
T├Łnh fŌĆ▓(ŽĆ) nß║┐u \(f(x) = \frac{{\sin x - x\cos x}}{{\cos x - x\sin x}}\)
-
B├Āi tß║Łp 35 trang 212 SGK To├Īn 11 NC
Giß║Żi phŲ░ŲĪng tr├¼nh yŌĆÖ = 0 trong mß╗Śi trŲ░ß╗Øng hß╗Żp sau :
a. y = sin2x - 2cosx
b. y = 3sin2x + 4cos2x + 10x
c. y=cos2x + sinx
d. y = tanx + cotx
-
B├Āi tß║Łp 36 trang 212 SGK To├Īn 11 NC
Cho h├Ām sß╗æ f(x) = 2cos2(4x ŌłÆ 1). Chß╗®ng minh rß║▒ng vß╗øi mß╗Źi x ta c├│ |fŌĆ▓(x)| Ōēż 8. T├¼m c├Īc gi├Ī trß╗ŗ cß╗¦a x ─æß╗ā ─æß║│ng thß╗®c xß║Ży ra.
-
B├Āi tß║Łp 37 trang 212 SGK To├Īn 11 NC
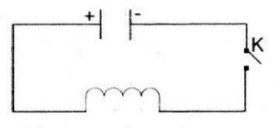
Cho mß║Īch ─æiß╗ćn nhŲ░ h├¼nh 5.7. L├║c ─æß║¦u tß╗ź ─æiß╗ćn c├│ ─æiß╗ćn t├Łch Q0. Khi ─æ├│ng kh├│a K, tß╗ź ─æiß╗ćn ph├│ng ─æiß╗ćn qua cuß╗Ön d├óy ; ─æiß╗ćn t├Łch q cß╗¦a tß╗ź ─æiß╗ćn phß╗ź thuß╗Öc v├Āo thß╗Øi gian t theo c├┤ng thß╗®c q(t) = Q0sinŽēt. Trong ─æ├│, Žē l├Ā tß╗æc ─æß╗Ö g├│c. Biß║┐t rß║▒ng cŲ░ß╗Øng ─æß╗Ö I(t) cß╗¦a d├▓ng ─æiß╗ćn tß║Īi thß╗Øi ─æiß╗ām t ─æŲ░ß╗Żc t├Łnh theo c├┤ng thß╗®c I(t) = qŌĆ▓(t) Cho biß║┐t Q0 = 10-8 v├Ā Žē = 106ŽĆ rad/s. H├Ży t├Łnh cŲ░ß╗Øng ─æß╗Ö cß╗¦a d├▓ng ─æiß╗ćn tß║Īi thß╗Øi ─æiß╗ām t = 6s (t├Łnh ch├Łnh x├Īc ─æß║┐n 10-5 mA)
-
B├Āi tß║Łp 38 trang 213 SGK To├Īn 11 NC
Cho h├Ām sß╗æ y = cos2x + msinx (m l├Ā tham sß╗æ) c├│ ─æß╗ō thß╗ŗ l├Ā (C). T├¼m m trong mß╗Śi trŲ░ß╗Øng hß╗Żp sau:
a. Tiß║┐p tuyß║┐n cß╗¦a (C) tß║Īi ─æiß╗ām vß╗øi ho├Ānh ─æß╗Ö x = ŽĆ c├│ hß╗ć sß╗æ g├│c bß║▒ng 1
b. Hai tiß║┐p tuyß║┐n cß╗¦a (C) tß║Īi c├Īc ─æiß╗ām c├│ ho├Ānh ─æß╗Ö x = ŌłÆŽĆ/4 v├Ā x = ŽĆ/3 song song hoß║Ęc tr├╣ng nhau.






