Phần hướng dẫn giải bài tập Toán 10 Bài 3 Công thức lượng giác sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Đại số 10 Cơ bản và Nâng cao.
-
Bài tập 1 trang 153 SGK Đại số 10
Tính
a) \(cos225^0 , sin240^0 , cot(-15^0 ), tan 75^0\);
b) \(sin \frac{7x}{12}, cos\left ( -\frac{\pi}{12} \right ),tan\left ( \frac{13\pi}{12} \right )\)
-
Bài tập 2 trang 153 SGK Đại số 10
Tính
a) \(cos(\alpha +\frac{\pi }{3})\), biết \(sin \alpha =\frac{1}{\sqrt{3}}\) và \(0 < \alpha < \frac{\pi}{2}\)
b) \(tan(\alpha -\frac{\pi }{4})\), biết \(cos\alpha = -\frac{1}{3}\) và \(\frac{\pi}{2} < \alpha < \pi\)
c) \(cos(a + b), sin(a - b),\) biết \(sina = \frac{4}{5}\), \(0^0 < a < 90^0\) và \(b=\frac{2}{3}, 90^0 < b < 180^0\)
-
Bài tập 3 trang 154 SGK Đại số 10
Rút gọn các biểu thức
a) \(sin(a + b) + sin(\frac{\pi}{2}- a)sin(-b)\)
b) \(cos(\frac{\pi}{4} + a)cos(\frac{\pi }{4}- a) + sin^2a\)\(cos( \frac{\pi}{4}+ a)cos(\frac{\pi}{4} - a) + \frac{1}{2} sin^2a\)
c) \(cos(\frac{\pi}{2} - a)sin(\frac{\pi }{2} - b) - sin(a - b)\)\(cos(\frac{\pi}{2} - a)sin(\frac{\pi}{2} - b) - sin(a - b)\)
-
Bài tập 4 trang 154 SGK Đại số 10
Chứng minh các đẳng thức
a) \(\frac{cos(a-b)}{cos(a+b)}=\frac{cotacotb+1}{cotacotb-1}\)
b) \(sin(a + b)sin(a - b) = sin^2a - sin^2b = cos^2b - cos^2a\)
c) \(cos(a + b)cos(a - b) = cos^2a - sin^2b = cos^2b -sin^2a\)
-
Bài tập 5 trang 154 SGK Đại số 10
Tính \(sin2a, cos2a, tan2a\), biết:
a) \(sina = -0,6\) và \(\pi < a < \frac{3\pi }{2}\);
b) \(cosa = -\frac{5}{13}\) và \(\frac{\pi }{2} < a < \pi\)
c) \(sina + cosa = \frac{1 }{2}\) và \(\frac{3\pi }{4} < a < \pi\)
-
Bài tập 6 trang 154 SGK Đại số 10
Cho sin \(2a = -\frac{5}{9}\) và \(\frac{\pi}{2} < a < \pi .\)
Tính \(sina\) và \(cosa\).
-
Bài tập 7 trang 155 SGK Đại số 10
Biến đổi thành tích các biểu thức sau
a) \(1 - sinx;\) b) \(1 + sinx;\)
c) \(1 + 2cosx;\) d) \(1 - 2sinx\)
-
Bài tập 8 trang 155 SGK Đại số 10
Rút gọn biểu thức \(A = \frac{{sinx + sin3x + sin5x}}{{cosx + cos3x + cos5x}}\)
-
Bài tập 6.30 trang 189 SBT Toán 10
Cho \(\cos \alpha = \frac{1}{3}\), tính \(\sin \left( {\alpha + \frac{\pi }{6}} \right) - \cos \left( {\alpha - \frac{{2\pi }}{3}} \right)\)
-
Bài tập 6.31 trang 190 SBT Toán 10
Cho \(\sin \alpha = \frac{8}{{17}},\sin \beta = \frac{{15}}{{17}}\) với \(0 < \alpha < \frac{\pi }{2},0 < \beta < \frac{\pi }{2}\). Chứng minh rằng \(\alpha + \beta = \frac{\pi }{2}\)
-
Bài tập 6.32 trang 190 SBT Toán 10
Chứng minh rằng các biểu thức sau là những hằng số không phụ thuộc α, β
a) \(\sin 6\alpha \cot 3\alpha - \cos 6\alpha\);
b) \({\left[ {\tan \left( {{{90}^0} - \alpha } \right) - \cot \left( {{{90}^0} + \alpha } \right)} \right]^2} - {\left[ {\cot \left( {{{180}^0} + \alpha } \right) + \cot \left( {{{270}^0} + \alpha } \right)} \right]^2}\);
c) \(\left( {\tan \alpha - \tan \beta } \right)\cot \left( {\alpha - \beta } \right) - \tan \alpha \tan \beta\);
d) \(\left( {\cot \frac{\alpha }{3} - \tan \frac{\alpha }{3}} \right).\tan \frac{{2\alpha }}{3}\)
-
Bài tập 6.33 trang 190 SBT Toán 10
Cho hình thang cân ABCD có đáy nhỏ AB = AD. Biết tanBDC = \(\frac{3}{4}\), tính các giá trị lượng giác của BAD.
-
Bài tập 6.34 trang 190 SBT Toán 10
Nếu \(\sin \alpha = \frac{2}{{\sqrt 5 }}\) thì cos2α bằng
A. 0,5 B. -0,25
C. \(\frac{3}{{\sqrt 5 }}\) D. -0,6
-
Bài tập 6.35 trang 190 SBT Toán 10
Biết sina + cosa = \(\frac{{\sqrt 2 }}{2}\). Giá trị sin2a là
A. \(\frac{{2\sqrt 2 }}{3}\)
B. \(\frac{2}{3}\)
C. \(\frac{{ - 1}}{2}\)
D. \(\frac{1}{2}\)
-
Bài tập 6.36 trang 190 SBT Toán 10
Cho \(\frac{\pi }{2} < \alpha < \frac{{3\pi }}{4}\). Giá trị \(\tan 2\alpha \) là
A. \( - 2\sqrt 7 \)
B. \(\frac{{3\sqrt 3 }}{4}\)
C. \( -3\sqrt 7 \)
D. \( 3\sqrt 7 \)
-
Bài tập 6.37 trang 190 SBT Toán 10
Cho \(0 < \alpha < \frac{\pi }{2}\). Biểu thức \(S = \frac{{\sin 4\alpha - 2\sin 2\alpha }}{{\sin 4\alpha + 2\sin 2\alpha }}\) có thể rút gọn thành biểu thức nào sau đây?
A. - tan2α B. tanα
C. cot2α D. cotα
-
Bài tập 6.38 trang 191 SBT Toán 10
Cho \(\tan 2\alpha = \frac{4}{3}\) với \(\frac{\pi }{2} < \alpha < \pi \). Giá trị \(\cos \alpha \) là
A. \(\frac{{ - \sqrt 5 }}{5}\) hoặc \(\frac{{2\sqrt 5 }}{5}\)
B. \(\frac{{ - \sqrt 5 }}{5}\)
C. \(\frac{{\sqrt 5 }}{5}\) hoặc \(\frac{{ - 2\sqrt 5 }}{5}\)
D. \(\frac{{\sqrt 5 }}{5}\)
-
Bài tập 6.39 trang 191 SBT Toán 10
Biết \(\sin a = - \frac{4}{5}\) với \(\frac{{3\pi }}{4} < a < \pi \). Giá trị tan a là
A. \(\frac{1}{2}\) B. 2
C. - 2 D. \(-\frac{1}{2}\)
-
Bài tập 6.40 trang 191 SBT Toán 10
Cho tanα = 2cotα và \(\frac{{3\pi }}{2}\) < α < 2π. Giá trị của biểu thức sinα + cosα là
A. \(\frac{{\sqrt 6 - \sqrt 3 }}{3}\)
B. \(\frac{{\sqrt 3 - \sqrt 6 }}{3}\)
C. \(\frac{{2 - \sqrt 3 }}{3}\)
D. \(\frac{{2 + \sqrt 3 }}{3}\)
-
Bài tập 6.41 trang 191 SBT Toán 10
Biết sinα - cosα = \(\frac{1}{2}\) và π < α < \(\frac{{5\pi }}{4}\). Giá trị cot2α là
A. \(\frac{{ - \sqrt 7 }}{3}\)
B. \(\frac{{1 - \sqrt 5 }}{3}\)
C. \(\frac{{2 - \sqrt 7 }}{3}\)
D. \(\frac{{\sqrt 7 }}{3}\)
-
Bài tập 38 trang 213 SGK Toán 10 NC
Hỏi mỗi khẳng định sau đây có đúng không? ∀α,∀β ta có:
\(\begin{array}{l}
a)\,2\cos \left( {\alpha + \beta } \right) = \cos \alpha + \cos \beta \\
b)\,\sin \left( {\alpha - \beta } \right) = \sin \alpha - \sin \beta \\
c)\,\sin \left( {\alpha + \beta } \right) = \sin \alpha .\cos \beta + \cos \alpha .\sin \beta \\
d)\,\cos \left( {\alpha - \beta } \right) = \cos \alpha .\cos \beta - \sin \alpha .\sin \beta \\
e)\,\frac{{\sin 4\alpha }}{{\cos 2\alpha }} = \tan 2\alpha \\
f)\,{\sin ^2}\alpha = \sin 2\alpha
\end{array}\) -
Bài tập 39 trang 213 SGK Toán 10 NC
Sử dụng 750 = 450 + 300, hãy tính giá trị lượng giác của góc 750
Sử dụng 150 = 450 - 300, hãy tính giá trị lượng giác của góc 150. (đối chiếu với kết quả bài tập 29)
-
Bài tập 40 trang 213 SGK Toán 10 NC
Chứng minh rằng:
\(\begin{array}{*{20}{l}}
{a){\mkern 1mu} {\mkern 1mu} \sin \alpha + \cos \alpha = \sqrt 2 \sin \left( {\alpha + \frac{\pi }{4}} \right)}\\
{b){\mkern 1mu} {\mkern 1mu} \sin \alpha - \cos \alpha = \sqrt 2 \sin \left( {\alpha - \frac{\pi }{4}} \right)}\\
\begin{array}{l}
c){\mkern 1mu} {\mkern 1mu} \tan \left( {\frac{\pi }{4} - \alpha } \right) = \frac{{1 - \tan \alpha }}{{1 + \tan \alpha }}\\
\left( {\alpha \ne \frac{\pi }{2} + k\pi ;\alpha \ne \frac{{3\pi }}{4} + k\pi } \right)
\end{array}\\
\begin{array}{l}
d){\mkern 1mu} {\mkern 1mu} \tan \left( {\frac{\pi }{4} + \alpha } \right) = \frac{{1 + \tan \alpha }}{{1 - \tan \alpha }}\\
\left( {\alpha \ne \frac{\pi }{2} + k\pi ;\alpha \ne \frac{\pi }{4} + k\pi } \right)
\end{array}
\end{array}\) -
Bài tập 41 trang 214 SGK Toán 10 NC
a) Biết \(\sin \alpha = \frac{1}{3};\alpha \in \left( {\frac{\pi }{2};\pi } \right)\). Hãy tính giá trị lượng của góc \(2\alpha \) và góc \(\frac{\alpha }{2}\)
b) Sử dụng \({15^0} = \frac{{{{30}^0}}}{2}\), hãy kiểm nghiệm lại kết quả của bài tập 39.
-
Bài tập 42 trang 214 SGK Toán 10 NC
Chứng minh rằng:
a) \(\sin \frac{{11\pi }}{{12}}{\rm{cos}}\frac{{5\pi }}{{12}} = \frac{1}{4}\left( {2 - \sqrt 3 } \right)\)
b) \({\rm{cos}}\frac{\pi }{7}{\rm{cos}}\frac{{3\pi }}{7}{\rm{cos}}\frac{{5\pi }}{7} = - \frac{1}{8}\)
c) \(\sin {6^0}\sin {42^0}\sin {66^2}\sin {78^0} = \frac{1}{16}\)
-
Bài tập 43 trang 214 SGK Toán 10 NC
Dùng công thức biến đổi tích thành tổng, chứng minh:
\(\begin{array}{*{20}{l}}
{a)\cos {{75}^0}\cos {{15}^0} = \sin {{75}^0}\sin {{15}^0} = \frac{1}{4}}\\
{b)\cos {{75}^0}\sin {{15}^0} = \frac{{2 - \sqrt 3 }}{4}}\\
{c)\sin {{75}^0}\cos {{15}^0} = \frac{{2 + \sqrt 3 }}{4}}\\
\begin{array}{l}
d)\cos \alpha \sin \left( {\beta - \gamma } \right) + \cos \beta \sin \left( {\gamma - \alpha } \right)\\
+ \cos \gamma \sin \left( {\alpha - \beta } \right) = 0,\forall \alpha ,\beta ,\gamma
\end{array}
\end{array}\) -
Bài tập 44 trang 214 SGK Toán 10 NC
Đơn giản các biểu thức sau:
a) \(\sin \left( {\frac{\pi }{3} + \alpha } \right) - \sin \left( {\frac{\pi }{3} - \alpha } \right)\)
b) \({\cos ^2}\left( {\frac{\pi }{4} + \alpha } \right) - {\cos ^2}\left( {\frac{\pi }{4} - \alpha } \right)\)
-
Bài tập 45 trang 214 SGK Toán 10 NC
Chứng minh rằng:
a) \(\frac{{\sin \alpha - \sin \beta }}{{\cos \alpha - \cos \beta }} = - \sqrt 3\)
nếu \(\left\{ \begin{array}{l}
\alpha + \beta = \frac{\pi }{3}\\
\cos \alpha \ne \cos \beta
\end{array} \right.\)b) \(\frac{{\cos \alpha - \cos 7\alpha }}{{\sin 7\alpha - \sin \alpha }} = \tan 4\alpha \)
(khi các biểu thức có nghĩa)
-
Bài tập 46 trang 215 SGK Toán 10 NC
Chứng minh rằng:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
a)\sin 3\alpha = 3\sin \alpha - 4{\sin ^3}\alpha ;\\
\cos 3\alpha = 4{\cos ^3}\alpha - 3\cos \alpha
\end{array}\\
\begin{array}{l}
b)\sin \alpha \sin \left( {\frac{\pi }{3} - \alpha } \right)\sin \left( {\frac{\pi }{3} + \alpha } \right)\\
= \frac{1}{4}\sin 3\alpha
\end{array}\\
\begin{array}{l}
{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \cos \alpha \cos \left( {\frac{\pi }{3} - \alpha } \right)\cos \left( {\frac{\pi }{3} + \alpha } \right)\\
= \frac{1}{4}\cos 3\alpha
\end{array}
\end{array}\)Ứng dụng: Tính sin 200 sin 400 sin 800 và tan 200 tan 400 tan 800
-
Bài tập 47 trang 215 SGK Toán 10 NC
Chứng minh rồi dùng máy tính bỏ túi hoặc bảng số để kiểm nghiệm lại gần đúng kết quả.
\(\begin{array}{*{20}{l}}
\begin{array}{l}
a)\cos {10^0}\cos {50^0}\cos {70^0}\\
= \sin {20^0}\sin {40^0}\sin {80^0} = \frac{{\sqrt 3 }}{8}
\end{array}\\
\begin{array}{l}
b)\sin {10^0}\sin {50^0}\sin {70^0}\\
= \cos {20^0}\cos {40^0}\cos {80^0} = \frac{1}{8}
\end{array}
\end{array}\) -
Bài tập 48 trang 215 SGK Toán 10 NC
Chứng minh rằng: \(\cos \frac{\pi }{7} + \cos \frac{{4\pi }}{7} + \cos \frac{{6\pi }}{7} = - \frac{1}{2}\)
Hướng dẫn: Nhân vế trái với \(\frac{\pi }{7}\) (hoặc \(\frac{2\pi }{7}\)) rồi sử dụng công thức biến đổi tích thành tổng.
-
Bài tập 49 trang 215 SGK Toán 10 NC
Chứng minh rằng giá trị của mỗi biểu thức sau không phụ thuộc vào x
\(\begin{array}{*{20}{l}}
\begin{array}{l}
a){\cos ^2}\left( {\alpha + x} \right) + {\cos ^2}x\\
- 2\cos \alpha \cos x.\cos \left( {\alpha + x} \right)
\end{array}\\
\begin{array}{l}
b)\sin 4x.\sin 10x - \sin 11x.\sin 3x\\
- \sin 7x.{\rm{sinx}}
\end{array}
\end{array}\) -
Bài tập 50 trang 215 SGK Toán 10 NC
Chứng minh rằng nếu tam giác ABC có 3 góc thỏa:
a) sin A = cos B + cos C thì tam giác ABC vuông
b) sin A = 2sin B.cos C thì tam giác ABC cân
-
Bài tập 51 trang 216 SGK Toán 10 NC
Chứng minh rằng nếu \(\alpha + \beta + \gamma = \pi \) thì:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
a)\sin \alpha + \sin \beta + \sin \gamma \\
= 4\cos \frac{\alpha }{2}\cos \frac{\beta }{2}\cos \frac{\gamma }{2}
\end{array}\\
\begin{array}{l}
b)\cos \alpha + \cos \beta + \cos \gamma \\
= 1 + 4\sin \frac{\alpha }{2}\sin \frac{\beta }{2}\sin \frac{\gamma }{2}
\end{array}\\
\begin{array}{l}
c)\sin 2\alpha + \sin 2\beta + \sin 2\gamma \\
= 4\sin \alpha \sin \beta \sin \gamma
\end{array}\\
\begin{array}{l}
d){\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\gamma \\
= 1 - 2\cos \alpha \cos \beta \cos \gamma
\end{array}
\end{array}\) -
Bài tập 52 trang 216 SGK Toán 10 NC
a) Chứng minh rằng nếu ∝ và β khác \(\frac{\pi }{2} + k\pi \) (k ∈ Z) thì:
\(\left\{ \begin{array}{l}
\tan \alpha + \tan \beta = \frac{{\sin \left( {\alpha + \beta } \right)}}{{\cos \alpha \cos \beta }}\\
\tan \alpha - \tan \beta = \frac{{\sin \left( {\alpha - \beta } \right)}}{{\cos \alpha \cos \beta }}
\end{array} \right.\)b) Chứng minh rằng với mọi ∝ mà cos k∝ ≠ 0 (k = 1, 2, 3, 4, 5, 6, 7, 8) và sin ∝ ≠ 0 thì:
\(\begin{array}{l}
\frac{1}{{\cos \alpha \cos 2\alpha }} + \frac{1}{{\cos 2\alpha \cos 3\alpha }} + ... + \\
\frac{1}{{\cos 7\alpha \cos 8\alpha }} = \frac{{\tan 8\alpha - \tan \alpha }}{{\sin \alpha }}
\end{array}\) -
Bài tập 53 trang 216 SGK Toán 10 NC
Biết cosα +cosβ = a; sinα+sinβ = b (a,b là hằng số và a2 + b2 ≠ 0)
Hãy tính sin(α + β) theo a và b
-
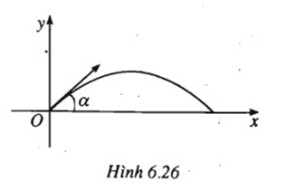
Bài tập 54 trang 216 SGK Toán 10 NC
Quỹ đạo của một vật được ném lên từ gốc O, với vận tốc ban đầu là v(m/s) theo phương hợp với trục hoành (nằm ngang) Ox một góc α ,\(0 < \alpha < \frac{\pi }{2}\) là parabol có phương trình :
\(y = - \frac{g}{{2{v^2}{\rm{co}}{{\rm{s}}^2}\alpha }}{x^2} + \left( {\tan \alpha } \right)x\)
Trong đó g là gia tốc trọng trường (g ≈ 9,8m/s2) (giả sử lực cản của không khí là không đáng kể).
Gọi tầm xa của quỹ đạo là khoảng cách từ O đến giao điểm khác O của quỹ đạo với Ox.
a) Tính tầm xa theo α (và v)
b) Khi v không đổi, α thay đổi trong khoảng \(\left( {0;\frac{\pi }{2}} \right)\), hỏi giá trị α nào thì tầm xa của quỹ đạo đạt được giá trị lớn nhất? Tính giá trị đó theo v. Khi v = 80m/s. Hãy tính giá trị lớn nhất đó (chính xác đến hàng đơn vị).