Bài tập 54 trang 216 SGK Toán 10 NC
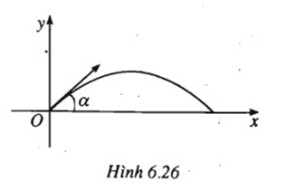
Quỹ đạo của một vật được ném lên từ gốc O, với vận tốc ban đầu là v(m/s) theo phương hợp với trục hoành (nằm ngang) Ox một góc α ,\(0 < \alpha < \frac{\pi }{2}\) là parabol có phương trình :
\(y = - \frac{g}{{2{v^2}{\rm{co}}{{\rm{s}}^2}\alpha }}{x^2} + \left( {\tan \alpha } \right)x\)
Trong đó g là gia tốc trọng trường (g ≈ 9,8m/s2) (giả sử lực cản của không khí là không đáng kể).
Gọi tầm xa của quỹ đạo là khoảng cách từ O đến giao điểm khác O của quỹ đạo với Ox.
a) Tính tầm xa theo α (và v)
b) Khi v không đổi, α thay đổi trong khoảng \(\left( {0;\frac{\pi }{2}} \right)\), hỏi giá trị α nào thì tầm xa của quỹ đạo đạt được giá trị lớn nhất? Tính giá trị đó theo v. Khi v = 80m/s. Hãy tính giá trị lớn nhất đó (chính xác đến hàng đơn vị).
Hướng dẫn giải chi tiết
a) Gọi x là tầm xa của quỹ đạo, thì:
\(\left\{ \begin{array}{l}
x > 0\\
- \frac{{g{x^2}}}{{2{v^2}{{\cos }^2}\alpha }} + \left( {\tan \alpha } \right)x = 0
\end{array} \right.\)
Tức là \(x = \frac{{2{v^2}\sin \alpha \cos \alpha }}{g} \)
\(= \frac{{{v^2}}}{g}\sin 2\alpha \)
b) x đạt giá trị lớn nhất khi và chỉ khi
\(\sin 2\alpha = 1 \Rightarrow \alpha = \frac{\pi }{4}\)
Khi đó: \(x = \frac{{{v^2}}}{g}\)
Với v = 80 m/s thì
\(\frac{{{v^2}}}{g} \approx \frac{{{{80}^0}}}{{9,8}} \approx 635\left( m \right)\)
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





