Giải bài 6.40 tr 191 SBT Toán 10
Cho tanα = 2cotα và \(\frac{{3\pi }}{2}\) < α < 2π. Giá trị của biểu thức sinα + cosα là
A. \(\frac{{\sqrt 6 - \sqrt 3 }}{3}\)
B. \(\frac{{\sqrt 3 - \sqrt 6 }}{3}\)
C. \(\frac{{2 - \sqrt 3 }}{3}\)
D. \(\frac{{2 + \sqrt 3 }}{3}\)
Hướng dẫn giải chi tiết
Ta có \(\tan \alpha = 2\cot \alpha = \frac{2}{{\tan \alpha }} \Rightarrow {\tan ^2}\alpha = 2\)
Vì \(\frac{{3\pi }}{2}\) < α < 2π nên \(\tan \alpha < 0\). Vậy \(\tan \alpha = - \sqrt 2 \)
\(\frac{1}{{{{\cos }^2}\alpha }} = 1 + {\tan ^2}\alpha = 3 \Rightarrow {\cos ^2}\alpha = \frac{1}{3}\)
Do đó \(\cos \alpha = \frac{{\sqrt 3 }}{3}\left( {do\,\cos \alpha > 0} \right)\)
Suy ra \(\sin \alpha = \tan \alpha .\cos \alpha = - \frac{{\sqrt 6 }}{3}\)
Vậy \(\sin \alpha + \cos \alpha = \frac{{\sqrt 3 - \sqrt 6 }}{3}\)
Đáp án B
-- Mod Toán 10 HỌC247
-


Tính cos(a+pi/3) biết sin anpha=1/căn 3
bởi Vy Vy Vy
 27/04/2020
27/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Rút gọn sin(a+b)+sin(a-b)/sin(a+b)-sin(a-b)
bởi Trinh Trinh
 18/04/2020
Giúp mình với
18/04/2020
Giúp mình với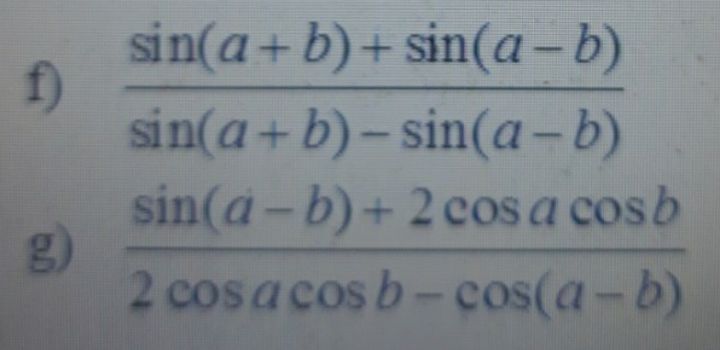 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh sinxcosx/(cos^2x-sin^2x)=tanx/(1-tan^2x)
bởi Châu Trần
 16/04/2020
16/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính số đo góc của tam giác ABC biết a=12, b=15, c=13
bởi Uyên nè
 07/04/2020
07/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh rằng: (tgA/4+tgB/4+tgC/4)+ (tgA/4*tgB/4+tgB/4*tgC/4+tgC/4*tgA/4)-(tgA/4*tgB/4*tgC/4)=1
bởi Nguyễn Anh Quân
 02/04/2020
02/04/2020
Chứng minh rằng:
(tgA/4+tgB/4+tgC/4)+ (tgA/4*tgB/4+tgB/4*tgC/4+tgC/4*tgA/4)-(tgA/4*tgB/4*tgC/4)=1
Theo dõi (1) 1 Trả lời -


Chứng minh nếu cos(A+C)+3cosB=1 thì B=60 độ
bởi Hạ Băng
 15/01/2020
Giúp e chứng minh bài 19b,c,d vs ạ
15/01/2020
Giúp e chứng minh bài 19b,c,d vs ạ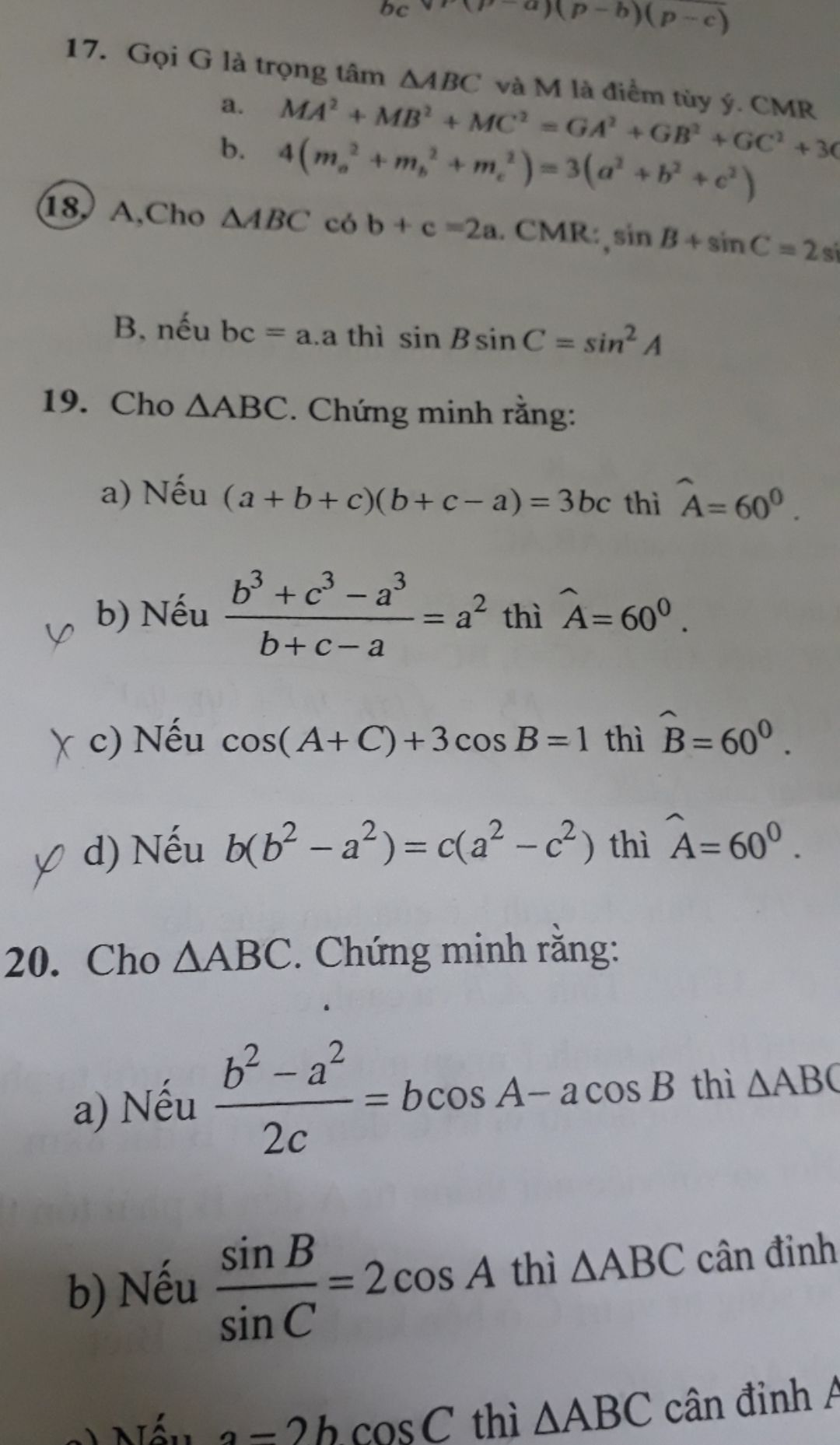 Theo dõi (0) 14 Trả lời
Theo dõi (0) 14 Trả lời
Bài tập SGK khác
Bài tập 6.38 trang 191 SBT Toán 10
Bài tập 6.39 trang 191 SBT Toán 10
Bài tập 6.41 trang 191 SBT Toán 10
Bài tập 38 trang 213 SGK Toán 10 NC
Bài tập 39 trang 213 SGK Toán 10 NC
Bài tập 40 trang 213 SGK Toán 10 NC
Bài tập 41 trang 214 SGK Toán 10 NC
Bài tập 42 trang 214 SGK Toán 10 NC
Bài tập 43 trang 214 SGK Toán 10 NC
Bài tập 44 trang 214 SGK Toán 10 NC
Bài tập 45 trang 214 SGK Toán 10 NC
Bài tập 46 trang 215 SGK Toán 10 NC
Bài tập 47 trang 215 SGK Toán 10 NC
Bài tập 48 trang 215 SGK Toán 10 NC
Bài tập 49 trang 215 SGK Toán 10 NC
Bài tập 50 trang 215 SGK Toán 10 NC
Bài tập 51 trang 216 SGK Toán 10 NC
Bài tập 52 trang 216 SGK Toán 10 NC





