Giải bài 48 tr 125 sách GK Toán 8 Tập 2
Tính diện tích toàn phần của:
a) Hình chóp tứ giác đều, biết cạnh đáy a = 5cm, cạnh bên b = 5cm, \(\sqrt{18,75} \approx 4,33\)
b) Hình chóp lục giác đều, biết cạnh đáy a = 6cm, cạnh bên b = 5cm, \(\sqrt{3} \approx 1,73\)
Hướng dẫn giải chi tiết
Câu a:
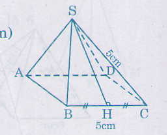
Từ đề bài ta có các mặt bên của hình chóp đều là những tam giác đều cạnh \(5cm\).
Đường cao của mỗi mặt bên là:
\(d=SH = \sqrt{SC^{2} -HC^{2}}\)
\(= \sqrt{5^{2} -2,5^{2}}= \sqrt{18,75}\approx 4,33 (cm) \)
Diện tích xung quanh hình chóp là:
\(S_{xq} = p.d = \dfrac{1}{2}. 5.4.4,33 = 43,3 (cm^2) \)
Diện tích đáy hình chóp:
\(S_{đ} = a^2 = 5^2 =25(cm^2) \)
Diện tích toàn phần hình chóp:
\( S_{tp} = S_{xq}+ S_{đ} = 43,3 + 25 = 68,3 \) \((cm^2)\)
Câu b:
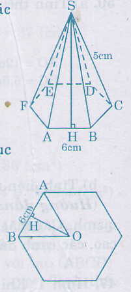
Mặt bên của hình chóp lục giác đều là tam giác cân có cạnh bên \(10cm\), cạnh đáy \(6cm\) .
Đường cao \(SH\) của mặt bên là:
\(d=SH = \sqrt{SA^{2} -AH^{2}} = \sqrt{10^{2} -3^{2}} \) \(= \sqrt{91}\approx 9,54 (cm) \)
Diện tích xung quanh hình chóp:
\(S_{xq} = p.d = \dfrac{1}{2}. 6.6.9,54 = 171,72\) \( (cm^2) \)
Đáy của hình chóp là lục giác đều. Diện tích lục giác bằng \(6\) lần diện tích tam giác đều \(ABO\).
Chiều cao của tam giác đều OAB là:
\(OH = \sqrt{OB^{2} -BH^{2}} = \sqrt{6^{2} -3^{2}}\) \(= \sqrt{27}\approx 5,2 (cm) \)
Diện tích đáy hình chóp:
\(S_{đ} =6.\dfrac{1}{2}.OH.AB=6. \dfrac{1}{2}5,2.6 = 93,6(cm^2) \)
Diện tích toàn phần hình chóp:
\( S_{tp} = S_{xq}+ S_{đ} = 171,72 + 93,6 \) \(= 265,32 (cm^2)\)
-- Mod Toán 8 HỌC247
-


Tìm x biết 4x^2 - 25 - (2x-5) (2x+7) = 0
bởi Lê Bảo An
 27/02/2019
27/02/2019
Tìm x:
a, 4x2 - 25 - (2x-5) (2x+7) = 0
b, 2x3 + 3x2 + 2x + 3 = 0
Theo dõi (0) 1 Trả lời -


Tìm min của P = x^2 + 2y^2 - 2xy + 8x + 8y + 2017
bởi bala bala
 27/02/2019
27/02/2019
giúp mình vs
P = x^2 + 2y^2 - 2xy + 8x + 8y + 2017
Theo dõi (0) 1 Trả lời -


Phân tích x^2-3xy^2-3x^2y - y^2 thành nhân tử
bởi Dương Minh Tuấn
 27/02/2019
27/02/2019
x2-3xy2-3x2y - y2
Theo dõi (0) 1 Trả lời -


Chứng minh x^2+y^2+z^2+3>=2(x+y+z)
bởi minh thuận
 27/02/2019
27/02/2019
x2+y2+z2+3>=2(x+y+z)
Theo dõi (0) 1 Trả lời -


Tính M= (x+y)^2007+(x-2)^2008+ (y+1)^2009 biết 5x^2+5y^2+8xy-2x+2y+2=0
bởi Đào Lê Hương Quỳnh
 27/02/2019
27/02/2019
5x2+5y2+8xy-2x+2y+2=0
Tính M= (x+y)2007+(x-2)2008+ (y+1)2009
Theo dõi (0) 1 Trả lời -


Tính M=a^4+b^4+c^4 biết a+b+c=0 và a^2+b^2+c^2=1
bởi hi hi
 27/02/2019
27/02/2019
Cho a+b+c=0 và a2+b2+c2=1. Tính M=a4+b4+c4
Theo dõi (0) 1 Trả lời -


Rút gọn biểu thức Q=(x+2)(x^2-2x+4)-x(x-2)(x+2)+2x
bởi Naru to
 27/02/2019
27/02/2019
Rút gọn biểu thức sau:
Q=\(\left(x+2\right)\left(x^2-2x+4\right)-x\left(x-2\right)\left(x+2\right)+2x\)
Theo dõi (0) 1 Trả lời -


Tính giá trị của biểu thức
x3 - 15x2+75x-125 tại x=35
Theo dõi (0) 1 Trả lời -


Tính (5-4x).(5+4x)-(4x-3)^2
bởi Hoa Lan
 27/02/2019
27/02/2019
(5-4x).(5+4x)-(4x-3)2
Theo dõi (0) 1 Trả lời -


Tìm x để x+2/x^3 =3
bởi Truc Ly
 27/02/2019
27/02/2019
Tìm x để x+2/x^3 =3
Theo dõi (0) 1 Trả lời -


tìm giá trị nhỏ nhất của biểu thức
( x - 1 ) ( x - 2 ) ( x - 3 ) (x - 4 ) + 2008
Theo dõi (0) 1 Trả lời -


Rút gọn các biểu thức (x - 3)(x + 2) - (x- 7)(x - 1)
bởi Lê Nhi
 27/02/2019
27/02/2019
Rút gọn các biểu thức sau :
a ) ( x - 3 )(x + 2) - (x - 7 )(x - 1)
b ) ( x - 2 )(x2 - 5x + 1 ) - x(x2 + 11)
Theo dõi (0) 1 Trả lời -


Chứng minh x^2+2y^2-2xy+2x-4y+3>0
bởi Nguyễn Trung Thành
 27/02/2019
27/02/2019
Chứng Minh x2+2y2-2xy+2x-4y+3>0 với mọi số thực x,y
Theo dõi (0) 1 Trả lời -


Tìm x biết (x - 2 )^2 - (x - 3).(x + 3)= 17
bởi Lê Tường Vy
 27/02/2019
27/02/2019
bài 1 : tìm x, biết
a, (x - 2 )^2 - (x - 3).(x + 3)= 17
b, 4(x - 3)^2 - (2x - 1).(2x + 1)= 10
c, (x - 4)^2 - (x - 2).(x + 2) = 36
d, (2x + 3)^2 - (2x - 1).(2x + 1) = 10
bài 2: cho biểu thức P = 3x^2 + 3x/(phần) (x+1).(2x - 6)
a, tìm điều kiện của x để biểu thức P xác định
b, tìm gtri của x sao cho P = 1
bài 3: cho biểu thức P= x/(phần) x-1 + x^2 + 1/(phần) 1- x^2
a, tìm x để biểu thức P có nghĩa
b, rút gọn biểu thức P
c, tìm giá trị của x sao cho P = -1
m.n ơi giúp em vs ạ em cảm ơn m,n nhìu
Theo dõi (0) 1 Trả lời -


Tìm x biết 2x+1/6 - x-2/4= 3-2x/3 -x
bởi Nguyễn Sơn Ca
 27/02/2019
giải pt: a)2x+1/6 - x-2/4= 3-2x/3 -x b)2x/x-1 + 4/x^2+2x-3 = 2x-5/x+3Theo dõi (0) 1 Trả lời
27/02/2019
giải pt: a)2x+1/6 - x-2/4= 3-2x/3 -x b)2x/x-1 + 4/x^2+2x-3 = 2x-5/x+3Theo dõi (0) 1 Trả lời -


Tìm x biết 2x^3 (2x-3) -x^2 (4x^2 -6x+2)=0
bởi hành thư
 27/02/2019
27/02/2019
a.2x^3 (2x-3) -x^2 (4x^2 -6x+2)=0
b.(x+3)^2 + (x-2) ( x+2) - 2(x-1)^2=7
c.(3x +2)(x-1) -3(x+1) (x-2) =4
giúp mình nha
Theo dõi (0) 1 Trả lời -


Cho a và b là hai số nguyên tố cùng nhau. Chứng minh 5a+3b và 13a+8b là 2 số nguyên tố cùng nhau.
Theo dõi (0) 1 Trả lời -


Tìm p nguyên tố sao cho 2^p+1chia hết cho p
bởi Trieu Tien
 27/02/2019
27/02/2019
Tìm p nguyên tố sao cho:
\(2^p+1⋮p\)
Theo dõi (0) 1 Trả lời -


Tìm 2 số nguyên tố P, Q sao cho P^2=8Q+1
bởi Lê Bảo An
 27/02/2019
27/02/2019
Tìm hai số nguyên tố P và Q sao cho P^2=8Q+1.
Theo dõi (0) 2 Trả lời -


Thực hiện phép tính (x^5 + 4x^3 - 6x^2) : 4x^2
bởi Nguyễn Trung Thành
 27/02/2019
27/02/2019
1. Làm tính nhân, chia:
a. (x5 + 4x3 - 6x2) : 4x2
b. (x3 - 8) : (x2 + 2x + 4)
c. (3x2 - 6x) : (2 - x)
d. (x3 + 2x2 - 2x - 1): (x2 + 3x + 1)
2. Tìm x, biết:
a. (x - 4)2 - (x - 2)(x + 2) = 6
b. 9 (x + 1)2 - (3x - 2)(3x + 2) = 10
Theo dõi (0) 1 Trả lời -


Tìm GTNN của biểu thức P= (2x-1)^2-(x+2)^2
bởi Lê Minh Trí
 27/02/2019
27/02/2019
Tìm GTNN:
a, P= (2x-1)2-(x+2)2
b, D= 2x2+2xy +2y2-6x-6y+5
Theo dõi (0) 1 Trả lời -


Tìm x biết 3x(x-5)-(3x+2)(3x-2)=31
bởi thu hảo
 27/02/2019
27/02/2019
I : Tìm x
1) 3x(x-5)-(3x+2)(3x-2)=31
2) (3x-1)(2x+7)-(x+1)(6x-5)=16
II: CMR
B=n(n+5)-(n-3)(n+20 chia hết cho 6 ( vs mọi N thuộc Z )
Theo dõi (0) 1 Trả lời -


Rút gọn biểu thức (x - 3)(x^2 +3x +9) - x(x^2 - 9)
bởi My Hien
 27/02/2019
27/02/2019
Rút gọn biểu thức:
b) (x - 3)(x2 +3x +9) - x(x2 - 9)
c) (x + 5)(x - 5) - (x - 3)(x + 2)
Theo dõi (0) 1 Trả lời -


Chứng minh x^2+3x+5 > 0 với mọi x
bởi Nhat nheo
 27/02/2019
27/02/2019
Chứng minh:
a/ \(^{x^2+3x+5}\) > 0 với mọi x
b/\(4x^2+5x+7\) > 0 với mọi x
c/\(6x-9x^2-4\) < 0 với mọi x
d/\(x-x^2-1\) < 0 với mọi x
e/\(2x-3x^2-5\) < 0 với mọi x
f/\(4x-5x^2-9\) < 0 với mọi x
Theo dõi (0) 1 Trả lời -


Tìm x biết 5(x+2)-x^2-2x=0
bởi Phan Thị Trinh
 27/02/2019
27/02/2019
Tìm x biết :5(x+2)-x2-2x=0
Theo dõi (0) 1 Trả lời -


Chứng minh 4x^2-xy+y^2>=0
bởi Mai Trang
 27/02/2019
27/02/2019
1) chứng minh:
a) 4x² - xy +y² ≥ 0
b) a² + b² + 2c² ≥ 2c(a+b)
c) a⁴ + b⁴ + c⁴ + d⁴ ≥ 4abcd
Theo dõi (0) 1 Trả lời -


Viết đa thức 8y^3 dưới dạng tích
bởi Nguyễn Lệ Diễm
 27/02/2019
27/02/2019
Viết đa thức sau dưới dạng tích
8y3- 1 =?
Ai bít giúp mk vs
Theo dõi (0) 1 Trả lời -


Chứng minh (6n+1)(n+5)-(3n+5)(2n-1) chia hết cho 2
bởi Bo bo
 27/02/2019
27/02/2019
chứng minh rằng với mọi số nguyên n thì
(6n+1)(n+5)-(3n+5)(2n-1) chia hết cho 2
Theo dõi (0) 1 Trả lời -


Phân tích x^2-4+(x-2)^2 thành nhân tử
bởi nguyen bao anh
 27/02/2019
27/02/2019
Phân tích thành nhân tử :
\(a.\) \(x^2-4+\left(x-2\right)^2\)
\(b.\) \(x^3-2x^2+x-xy^2\)
\(c.\) \(x^3-4x^2-12x+27\)
Theo dõi (0) 1 Trả lời -


Phân tích đa thức x -xy + y - y^2 thành nhân tử
bởi Bánh Mì
 27/02/2019
27/02/2019
Phân tích các đa thức sau thành nhân tử:
a) x -xy + y - y2
b) x2 - 4x - y + 4
Giúp mk vs
Theo dõi (0) 1 Trả lời -


Tìm x biết 2x^2+3.(x^2-1)=5x.(x+1)
bởi Nguyễn Trọng Nhân
 27/02/2019
27/02/2019
Ai giúp e với
1. Tìm x
a)2x^2+3.(x^2-1)=5x.(x+1)
b)2x.(5-3x)+2.(3x-5)-3.(x-7)=3
c)6x^2-(2x-3).(3x+2)-1=0
d)(x-3).(x+7)-(x+5).(x-1)=0
Ai làm nhanh, kĩ, chính xác nhất thì ib sẽ nhận được 1 thẻ đt. Chốt 10h30" tối. Trao giải 9h sáng mai.
Theo dõi (0) 1 Trả lời -


Phân tích x^4 - 4x^2 - 6x +12 thành nhân tử
bởi Nguyễn Hạ Lan
 27/02/2019
27/02/2019
phân tích đa thức thành nhân tử
x4 - 4x2 - 6x +12
Theo dõi (0) 1 Trả lời -


phân tích thành nhân tử
6x4+5x3-38x2+5x+6
Theo dõi (0) 1 Trả lời -


Tính 3a^2-3ab-5a+5b
bởi Nguyễn Tiểu Ly
 27/02/2019
27/02/2019
tính:
3a2-3ab-5a+5bTheo dõi (0) 1 Trả lời -


Phân tích đa thức 6x^2+12x+6 thành nhân tử:
bởi Nguyễn Thị An
 27/02/2019
27/02/2019
phân tích đa thức thành nhân tử:
\(6x^2+12x+6\)
Theo dõi (0) 1 Trả lời -


Chứng minh a^7-a chia hết cho 42
bởi Lê Nhật Minh
 27/02/2019
27/02/2019
Chứng minh a7-a chia hết cho 42
Theo dõi (0) 1 Trả lời -


Tính 0,5 x^2y( 2x^3 - 0,4 xy^2 - 1)
bởi Đan Nguyên
 27/02/2019
27/02/2019
a)0,5 x2y( 2x3 - 0,4 xy2 - 1)
b) (x2 - 1 )(x2 + 2x - 1)
Theo dõi (0) 1 Trả lời -


Tìm x biết 2x .(5-3x)+2x .(3x-5)-3(x-7)=3
bởi Ha Ku
 27/02/2019
27/02/2019
Tìm x ,biết
a)2x .(5-3x)+2x .(3x-5)-3(x-7)=3
b)3x .(x+1)-2x .(x+2)=-1-x
Theo dõi (0) 1 Trả lời -


Tìm m để m^2x+2x = 5+3mx vô nghiệm
bởi Tra xanh
 27/02/2019
27/02/2019
tìm giá trị của m để phương trình sau vô nghiệm:
m2x+2x = 5+3mx
Theo dõi (0) 1 Trả lời -


Khai triển (ax+7)^2
bởi Nguyễn Xuân Ngạn
 27/02/2019
27/02/2019
a)(ax+7)2
b)(6x-\(\dfrac{1}{3}\)y)2
c)1012
d)992
Theo dõi (0) 1 Trả lời -


Tìm a, b để x^4 + 4 chia cho hết x^2 + ax + b
bởi Lê Tấn Vũ
 27/02/2019
27/02/2019
Đề bài: Xác định hằng số a và b sao cho x^4 + 4 chia cho hết x^2 + ax + b
Theo dõi (0) 1 Trả lời -


bài 1 : Rút gọn rồi tính biểu thức sau :
a) 4x(3x - 2 ) - 3x(4x + 1) với x = -2
b) (x + 3) (x - 3) - (x - 1) 2 với x = 6
bài 2 : Phân tích các đa thức sau thành nhân tử
a) x2 - 4x + 4
b) x3 - 5x2 + x - 5
Theo dõi (0) 1 Trả lời -


Tìm số nguyên x biết 2x^2+ x- 18 chia hết cho x- 3
bởi Chai Chai
 27/02/2019
27/02/2019
Tìm x thuộc Z để:
2x2+ x- 18 chia hết cho x- 3
Theo dõi (0) 1 Trả lời -


Tìm GTNN của biểu thức P=x^2+2y^2+2xy-6x-4y+13
bởi Nguyễn Vân
 27/02/2019
27/02/2019
Tìm GTNN của biểu thức \(P=x^2+2y^2+2xy-6x-4y+13\)
Theo dõi (0) 1 Trả lời -


Tìm x biết 4^x-10.2^x+16=0
bởi hi hi
 27/02/2019
27/02/2019
\(4^x-10\times2^x+16=0\)
Theo dõi (0) 1 Trả lời -


Tìm x,y,z biết x^2-6x+y^2+10y+34= -(4z-1)^2
bởi Thụy Mây
 27/02/2019
27/02/2019
Tìm x,y,z
x2-6x+y2+10y+34= -(4z-1)2
Theo dõi (0) 1 Trả lời -


Chứng minh n^4-1 chia hết cho 48
bởi Lê Vinh
 27/02/2019
27/02/2019
1/ Cho \(n\) lẻ và \((n,3)=1\). chứng minh \(n^4-1 \ \vdots \ 48\)
2/ Cho n lẻ và (n,5)=1. chứng minh \( n^4-1 \ \vdots \ 80\)
3/ cmr: \(n^6+n^4-2n^2\) chia hết cho 72
4/ cm : \(n^8-n^4\) chia hết cho 240Theo dõi (0) 1 Trả lời -


Chứng minh a^2+b^2-2ab thì a=b
bởi thu hảo
 27/02/2019
27/02/2019
cmr \(a^2+b^2=2ab\) thì \(a=b\)
Theo dõi (0) 1 Trả lời -


Giải phương trình sau 5-(x-6) = 4(3-2x)
bởi na na
 27/02/2019
27/02/2019
Giải phương trình sau :
5-(x-6) = 4(3-2x)
Theo dõi (0) 1 Trả lời -


Tìm x để P=-|x-3|+12 đạt giá trị lớn nhất
bởi Bình Nguyen
 27/02/2019
27/02/2019
Giá trị của x để biểu thức : P= -\(\left|x-3\right|\)+12 đạt giá trị lớn nhất
Theo dõi (0) 1 Trả lời -


Tìm x biết x^4 + 5x^3 + 10x - 4 = 0
bởi Lê Tấn Vũ
 27/02/2019
27/02/2019
Tìm x, biết:
x4 + 5x3 + 10x - 4 = 0.
Theo dõi (0) 1 Trả lời -


Tìm GTNN của biểu thức D= x(x+6)
bởi Phạm Phú Lộc Nữ
 27/02/2019
27/02/2019
Tìm GTNN
D= x(x+6)
Theo dõi (0) 1 Trả lời -


Tìm x, y nguyên biết (x^2+y^2)(x+y)=20001
bởi Phạm Khánh Ngọc
 27/02/2019
27/02/2019
Tìm x,y nguyên
(x2+y2)(x+y)=20001
Theo dõi (0) 1 Trả lời -


Giải phương trình (x-3)(x-5)(x-6)(x-10)=24x^2
bởi Mai Vàng
 27/02/2019
27/02/2019
Giải phương trình : \(\left(x-3\right)\left(x-5\right)\left(x-6\right)\left(x-10\right)=24x^2\)
Theo dõi (0) 1 Trả lời -


Rút gọn (x - 1) (x^3 + x^2 + x +1)
bởi Aser Aser
 27/02/2019
27/02/2019
1. Rút gọn
a. ( x - 1) ( x3 + x 2 + x +1)
b. ( x - 2) ( x2 + x + 1) - x ( x2 - 1)
2. Tìm x
a. (x + 1) ( x + 2) + ( 1- x) (x -2 ) = 7
b. ( x +2 ) (x + 3) - ( x - 3) ( x + 4) = 5
Theo dõi (0) 1 Trả lời -


Tìm x, y là số nguyên tố để x^2 - 2y^2 = 1
bởi Sam sung
 27/02/2019
27/02/2019
Tìm x,y là số nguyên tố để :
x2 - 2y2 = 1
Theo dõi (0) 1 Trả lời -


Tìm số tự nhiên n để n^2+1234 là số chính phương
bởi Việt Long
 27/02/2019
27/02/2019
Tìm tất cả n\(\in\) N sao cho \(n^2+1234\) là số chính phương
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 46 trang 124 SGK Toán 8 Tập 2
Bài tập 47 trang 124 SGK Toán 8 Tập 2
Bài tập 49 trang 125 SGK Toán 8 Tập 2
Bài tập 50 trang 125 SGK Toán 8 Tập 2
Bài tập 62 trang 150 SBT Toán 8 Tập 2
Bài tập 63 trang 151 SBT Toán 8 Tập 2
Bài tập 64 trang 151 SBT Toán 8 Tập 2
Bài tập 65 trang 151 SBT Toán 8 Tập 2
Bài tập 66 trang 152 SBT Toán 8 Tập 2
Bài tập 67 trang 152 SBT Toán 8 Tập 2
Bài tập 68 trang 152 SBT Toán 8 Tập 2
Bài tập 69 trang 152 SBT Toán 8 Tập 2
Bài tập 70 trang 153 SBT Toán 8 Tập 2





