Giải bài 23 tr 47 sách GK Toán 8 Tập 2
Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:
a) 2x - 3 > 0; b) 3x + 4 < 0;
c) 4 - 3x ≤ 0; d) 5 - 2x ≥ 0.
Hướng dẫn giải chi tiết
Câu a:
2x - 3 > 0 ⇔ 2x > 3 <=> x > 
Vậy tập nghiệm của bất phương trình là S = {x/x > } và được biểu diễn trên trục số như sau:
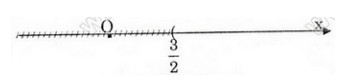
Câu b:
3x + 4 < 0 ⇔ x <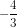 
Vậy tập nghiệm của bất phương trình là S = {x/x < } và được biểu diến trên trục số như sau:
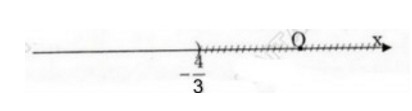
Câu c:
4 - 3x ≤ 0 ⇔ x ≥ 
Vậy tập nghiệm của bất phương trình là S = {x/x ≥ } và được biểu diễn trên trục số như sau:
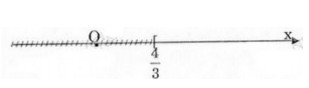
Câu d:
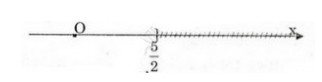
5 - 2x ≥ 0 ⇔ 5 ≥ 2x ⇔ x ≤ 
Vậy tập nghiệm của bất phương trình là S = {x/x ≤ } và được biểu diến trên trục số như sau:
-- Mod Toán 8 HỌC247
-
A. A = 6x - 1
B. A = 1 - 2x
C. A = - 1 - 2x
D. A = 1 - 6x
Theo dõi (0) 2 Trả lời -
Tìm tất cả các giá trị của tham số m để bất phương trình m( x - 1 ) < 3 - x có nghiệm?
bởi Lê Bảo An
28/05/2020
Theo dõi (0) 1 Trả lời -
Bất phương trình m^2( x - 1 ) ≥ 9x + 3m có nghiệm đúng với mọi x khi nào?
bởi Trần Hoàng Mai
28/05/2020
Theo dõi (0) 1 Trả lời -
A. m ≠ 1
B. m ≠ 2
C. m = 1,m = 2
D. m ∈ R
Theo dõi (0) 1 Trả lời -
Giải BPT \({x^2}+6x+8 < 0\)?
bởi Quỳnh Vân
25/05/2020
Theo dõi (0) 0 Trả lời -
Chứng minh rằng \(\frac{{{a^2} + {b^2}}}{2} \ge {\left( {\frac{{a + b}}{2}} \right)^2}\)?
bởi Lưu Trung Hiếu
17/05/2020
Theo dõi (0) 0 Trả lời -
Giải bất phương trình x+5/3<0
bởi Hương Giang
15/05/2020
Theo dõi (0) 1 Trả lời -
Giải phương trình |x-9I =2x+5
bởi Trần Xuân
13/05/2020
Bài 1:giải các phương trình:A,I x-9 I =2x 5B,2/x-3 3/x 3=3x 5/x mũ hai-9Theo dõi (0) 2 Trả lời -
(x/x+3+3-x/x+3.x^2+3x+9/x^2-9):3/x+3
Theo dõi (0) 0 Trả lời -
Giải các bất phương trình sau?
bởi Ngân Cindy
07/05/2020
Mng giúp em bài tập này với ạ. Biết câu nào chỉ câu đó cũng được ạ :(( E camonnn mng nhìu
Theo dõi (0) 2 Trả lời -
Giả bất phương trình x-2>4
bởi Ngô Phương Thảo
26/04/2020
Giúp mk với
Theo dõi (0) 3 Trả lời
