Giải bài 58 tr 18 sách BT Toán lớp 7 Tập 1
Hình vuông dưới đây có tính chất: mỗi ô ghi một lũy thừa của \(10\); tích các số trong mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau. Hãy điền các số còn thiếu vào các ô trống:
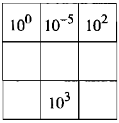
Hướng dẫn giải chi tiết
Hướng dẫn giải
Áp dụng các công thức:
\({x^m}.{x^n} = {x^{m + n}}\)
\({x^m}:{x^n} = {x^{m - n}}\)
Lời giải chi tiết
Xét tích các số ở hàng thứ nhất ta được: \({10^0}{.10^{ - 5}}{.10^2} = {10^{0 + \left( { - 5} \right) + 2}} = {10^{ - 3}}\)
Ta có tích các số trong mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau (bằng \({10^{ - 3}}\)).
Xét cột thứ hai, ô trống thứ hai cần điền có giá trị là: \({10^{ - 3}}:\left( {{{10}^{ - 5}}{{.10}^3}} \right) = {10^{ - 3}}:{10^{ - 2}} \)\(\,= {10^{\left( { - 3} \right) - \left( { - 2} \right)}} = {10^{ - 1}}\)
Xét đường chéo thứ nhất, ô trống cần điền có giá trị là: \({10^{ - 3}}:\left( {{{10}^0}{{.10}^{ - 1}}} \right) = {10^{ - 3}}:{10^{ - 1}} \)\(\,= {10^{\left( { - 3} \right) - \left( { - 1} \right)}} = {10^{ - 2}}\)
Xét cột thứ ba, ô trống thứ ba cần điền có giá trị là: \({10^{ - 3}}:\left( {{{10}^2}{{.10}^{ - 2}}} \right) = {10^{ - 3}}:{10^0} = {10^{ - 3}}\)
Xét hàng thứ hai, ô trống thứ nhất cần điền có giá trị là: \({10^{ - 3}}:\left( {{{10}^{ - 3}}{{.10}^{ - 1}}} \right) = {10^{ - 3}}:{10^{ - 4}} \)\(\,= {10^{\left( { - 3} \right) - \left( { - 4} \right)}} = {10^1}\)
Xét hàng thứ ba, ô trống thứ nhất cần điền có giá trị là: \({10^{ - 3}}:\left( {{{10}^3}{{.10}^{ - 2}}} \right) = {10^{ - 3}}:{10^1} \)\(\,= {10^{\left( { - 3} \right) - 1}} = {10^{ - 4}}\)
Ta được bảng sau:
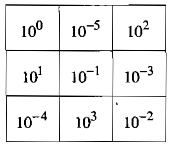
-- Mod Toán 7 HỌC247
-


Tìm n để P=n+2/n-7 có giâ trị lớn nhất
bởi Nguyễn Minh Minh
 18/01/2019
18/01/2019
tìm n để
\(p=\dfrac{n+2}{n-7}\)có giá trị lớn nhất
Theo dõi (0) 1 Trả lời -


Tìm x, y, z biết 3(x-1)=2(y-2)=3(z-3) và 2x +4y -z=50
bởi thanh duy
 18/01/2019
18/01/2019
tìm x,y,z biết 3(x-1)=2(y-2)=3(z-3) và 2x +4y -z=50
Theo dõi (0) 1 Trả lời -


Chứng minh 3^n+3+3^n+1+2^n+3+2^n+2 chia hết cho 6
bởi Phạm Khánh Ngọc
 18/01/2019
18/01/2019
Chứng minh:\(3^{n+3}+3^{n+1}+2^{n+3}+2^{n+2}⋮6\)
Theo dõi (0) 1 Trả lời -


c/m nếu a,b \(\in Z\) và a+b \(⋮3\) thì a3+b3\(⋮3^2\)
Theo dõi (0) 1 Trả lời -


Tìm nghiệm của đa thức Q(x) = 2x^2 + 3x
bởi Nguyễn Thị An
 18/01/2019
18/01/2019
a/ Tìm nghiệm của đa thức : Q(x) = 2x^2 + 3x
b/ Chứng minh đa thức x^2 +4x + 5 không có nghiệm
Theo dõi (0) 1 Trả lời -


Tìm x biết 8/7x-10/3=-5/21
bởi Quế Anh
 18/01/2019
18/01/2019
8/7x-10/3=-5/21
x:27=-2:3,6
Theo dõi (0) 1 Trả lời -


Tìm giá trị nhỏ nhất của biểu thức P=|x-7|+6-x
bởi Lan Anh
 18/01/2019
18/01/2019
tìm giá trị nhỏ nhất của biểu thức P=|x-7|+6-x và giá trị của x tương ứng
Theo dõi (0) 1 Trả lời -


Tìm nghiệm của đa thức A(x)=3x^2-15x
bởi Phong Vu
 18/01/2019
18/01/2019
Tìm nghiệm của đa thức. A(x)=3x^2-15x ;. B(x)=-2x^2-1. C(x)=2x^3+18x.
Theo dõi (0) 1 Trả lời -


Bài I.7* trang 35 sách bài tập toán 7 tập 1
bởi Nguyễn Xuân Ngạn
 18/01/2019
Bài I.7* - Bài tập bổ sung (Sách bài tập - tập 1 - trang 35)
18/01/2019
Bài I.7* - Bài tập bổ sung (Sách bài tập - tập 1 - trang 35)Với giá trị nào của \(x\) thì \(B=\left|x-1\right|+\left|x-2\right|+\left|x-3\right|+\left|x-5\right|\) đạt giá trị nhỏ nhất ?
Theo dõi (0) 1 Trả lời -


Tìm nghiệm của đa thức B=x+2(x+1)^2-2
bởi Nguyễn Minh Hải
 18/01/2019
18/01/2019
Tìm nghiệm của đa thức:
\(B=x+2\left(x+1\right)^2-2\)
\(C=x^4.\left(x+2\right)-x^2\)
\(D=3\left|x+2\right|+6\left(x+2\right)^8+6\)
\(H=4\left(x+5\right)^2-2\left|x+3\right|+12\)
Theo dõi (0) 1 Trả lời -


Bài I.6* trang 35 sách bài tập toán 7 tập 1
bởi Nguyễn Thị Trang
 18/01/2019
Bài I.6* - Bài tập bổ sung (Sách bài tập - tập 1 - trang 35)
18/01/2019
Bài I.6* - Bài tập bổ sung (Sách bài tập - tập 1 - trang 35)Với giá trị nào của \(x\) thì \(A=\left|x-3\right|+\left|x-5\right|+\left|x-7\right|\) đạt giá trị nhỏ nhất ?
Theo dõi (0) 1 Trả lời -


Tìm các số nguyên x, y biết x-2xy+y-3=10
bởi Kim Ngan
 18/01/2019
18/01/2019
Tìm các số nguyên x,y biết: x-2xy+y-3=10
Theo dõi (0) 1 Trả lời -


Bài I.5* trang 34 sách bài tập toán 7 tập 1
bởi trang lan
 18/01/2019
Bài I.5* - Bài tập bổ sung (Sách bài tập - tập 1 - trang 34)
18/01/2019
Bài I.5* - Bài tập bổ sung (Sách bài tập - tập 1 - trang 34)Tìm \(x,y\) biết :
\(\dfrac{x^2+y^2}{10}=\dfrac{x^2-2y^2}{7}\) và \(x^4y^4=81\)
Theo dõi (0) 1 Trả lời -


Bài I.4* trang 34 sách bài tập toán 7 tập 1
bởi Việt Long
 18/01/2019
Bài I.4* - Bài tập bổ sung (Sách bài tập - tập 1 - trang 34)
18/01/2019
Bài I.4* - Bài tập bổ sung (Sách bài tập - tập 1 - trang 34)Cho :
\(a+b+c=a^2+b^2+c^2=1\)
và
\(x:y:z=a:b:c\)
Chứng minh rằng :
\(\left(x+y+z\right)^2=x^2+y^2+z^2\)
Theo dõi (0) 1 Trả lời -

 Bài I.2 - Bài tập bổ sung (Sách bài tập - tập 1 - trang 34)
Bài I.2 - Bài tập bổ sung (Sách bài tập - tập 1 - trang 34)Thương \(\dfrac{12^{30}}{36^{15}}\) bằng :
(A) \(4^{15}\) (B) \(\left(\dfrac{1}{3}\right)^{15}\) (C) \(\left(\dfrac{1}{3}\right)^2\) (D) 1
Hãy chọn đáp án đúng ?
Theo dõi (0) 1 Trả lời -


Cho đa thức A(x) = - ( 2x^4 + 7x^5 - 3x^2 ) + 2x^4 + 7x^5 -2x^2 +1 và đa thức G(x) = x^2 + x+2
a. Thu gọn A(x)
b. Tìm x để A(x) = G(x)
c. Chứng tỏ A(x) không có nghiệm
Theo dõi (0) 1 Trả lời -


Tính A=(5.(3y/5)^2+3y'^2)/(10(3y/5)^2-3y^2)
bởi Lê Nhật Minh
 25/05/2019
25/05/2019
Tính a
A=\(\frac{5.\left(\frac{3.y}{5}\right)^2+3.y^2}{10.\left(\frac{3.y}{5}\right)^2-3.y^2}\)
Theo dõi (0) 1 Trả lời -


Tính 2010^H biết H=2^2010-2^2009-2^2008-...-2-1
bởi het roi
 25/05/2019
25/05/2019
a. Cho H= \(2^{2010}-2^{2009}-2^{2008}-...-2-1\)
Tính \(2010^H\)
b. Cho 3 số x,y,z là 3 số khác 0 thỏa mãn điều kiện \(\dfrac{y+z-x}{x}=\dfrac{z+x-y}{y}=\dfrac{x+y-z}{z}\)
Hãy tính giá trị biểu thức
B=\(\left(1+\dfrac{x}{y}\right)+\left(1+\dfrac{y}{z}\right)+\left(1+\dfrac{z}{x}\right)\)
Giúp mình nha. Bí quá
Theo dõi (0) 1 Trả lời -


Chứng minh A= (-7) + (-7)^2 + (-7)^3 + ... + (-7)^2006 chia hết cho 43
bởi nguyen bao anh
 25/05/2019
25/05/2019
1. a) \(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{99.100}\)
b) 6. \(\left(\frac{-1}{3}\right)^2\) - \(\left(\frac{1}{4}:2-\frac{7}{16}.\frac{-4}{21}\right)\)
2. Cho ba số a, b, c tỉ lệ với các số 2, 4, 5 và a - 20 = 24 (b +c). Tìm ba số a, b, c.
3.
a) Cho A= (-7) + (-7)2 + (-7)3 + ... + (-7)2007. CMR A chia hết cho 43.
b) Tìm các giá trị của x, y thỏa mãn: l2x -27l2011 + (3y +10)2012 = 0.
LÀM ĐC BÀI NÀO THÌ LÀM GIÚP NHA MN, HU HU HU! CẢM ƠN CÁC BẠN NHIỀU!
Theo dõi (0) 2 Trả lời -


Tìm x, biết 3^x+3^(x+1)=3^(x+2)=117
bởi hà trang
 05/12/2019
05/12/2019
Tìm \(x;\)biết:
\(3^x+3^{x+1}+3^{x+2}=117\)
Theo dõi (0) 1 Trả lời -


Tính C=(3/4-81).(3^2/5-81)...(3^2013/2016-81)
bởi het roi
 10/12/2019
10/12/2019
\(C=\left(\frac{3}{4}-81\right)\left(\frac{3^2}{5}-81\right)\left(\frac{3^3}{6}-81\right)...\left(\frac{3^{2013}}{2016}-81\right)\)
Theo dõi (0) 1 Trả lời -


Tìm x, y biết 5x=2y và x-y=99
bởi Thiên Mai
 21/01/2019
21/01/2019
Tìm x, y biết 5x=2y và x-y=99
Theo dõi (0) 1 Trả lời -


Tìm số mà bình phương của nó bằng chính nó
bởi Nguyễn Thị Lưu
 21/01/2019
21/01/2019
Đố em tìm được số mà :
a) Bình phương của nó bằng chính nó
b) Lập phương của nó bằng chính nó
Theo dõi (0) 1 Trả lời -


Tìm x, y biết:
Ix-2013I + Ix-2014I + Iy-2015I + Ix-2016I = 3
Theo dõi (0) 1 Trả lời -


Tính A=1+3/2^3+4/2^4+...+100/2^100
bởi Lê Vinh
 21/01/2019
21/01/2019
tinh a=1+3/2^3+4/2^4+...+100/2^100
Theo dõi (0) 1 Trả lời -


Tìm chữ số tận cùng của 2008^2014
bởi Tuấn Huy
 21/01/2019
21/01/2019
Bài 1:tìm các số tận cùng của :
a,20082014
b,9992003
Bài 2:CMR:
a,34n+1+2chia hết cho 5
b,92n+1+1 chia hết cho 10
Theo dõi (0) 1 Trả lời -


Bài III.2 trang 54 sách bài tập toán 7 tập 2
bởi Mai Anh
 21/01/2019
Bài III.2 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 54)
21/01/2019
Bài III.2 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 54)Cho tam giác ABC có hai đường trung tuyến AD, BE vuông góc với nhau. Chứng minh rằng BC < 2AC ?
Theo dõi (0) 1 Trả lời -


Tính giá trị biểu thức M=x^4-xy^3+x^3y-y^4-1 biết x+y=0
bởi Sasu ka
 21/01/2019
21/01/2019
Nếu x+y=0 thì giá trị của biểu thức M=x4-xy3+x3y-y4-1
Theo dõi (0) 1 Trả lời -


Bài 89 trang 53 sách bài tập toán 7 tập 2
bởi Thu Hang
 21/01/2019
Bài 89 (Sách bài tập - tập 2 - trang 53)
21/01/2019
Bài 89 (Sách bài tập - tập 2 - trang 53)Cho hình 20 :
Trong đó giao điểm O của hai đường thẳng a và b nằm ngoài phạm vi tờ giấy. Chỉ vẽ hình trong phạm vi tờ giấy, hãy vẽ đường thẳng d đi qua A sao cho đường thẳng d cũng đi qua O nếu kéo dài đường thẳng d ra ngoài phạm vi tờ giấy.
Theo dõi (0) 1 Trả lời -


Tìm GTNN của biểu thức B= 1-(2x-1)^2
bởi Nhat nheo
 21/01/2019
21/01/2019
Tìm GTNN của:
A=\(\dfrac{2009}{2009+\left(x+1\right)^2}\)
B= 1-(2x-1)2
Theo dõi (0) 1 Trả lời -


Cho A(x) = 2x2 - 8 +\(\dfrac{1}{2}\)x3 + 8
Tìm nghiệm của A(x) sao cho x>-4
Theo dõi (0) 1 Trả lời -


Tìm nghiệm của các đa thức sau :
A = \(\left|x-2017\right|+\left|x-2016\right|\)
f(x) = 3x . (x-2) - x . (3x+1) - 14
g(x) = x^2 - 2x + 2
Theo dõi (0) 1 Trả lời -


Bài 88 trang 53 sách bài tập toán 7 tập 2
bởi Hy Vũ
 21/01/2019
Bài 88 (Sách bài tập - tập 2 - trang 53)
21/01/2019
Bài 88 (Sách bài tập - tập 2 - trang 53)Cho góc xOy khác góc bẹt. Dùng một chiếc thước thẳng có chia khoảng, hãy nêu cách vẽ tia phân giác của góc xOy ?
Theo dõi (0) 1 Trả lời -


Tìm x biết |x+3|+|x+1|=3x
bởi hành thư
 21/01/2019
21/01/2019
\(\left|x+3\right|+\left|x+1\right|=3x\)
Theo dõi (0) 1 Trả lời -


Bài 87 trang 53 sách bài tập toán 7 tập 2
bởi Hoa Hong
 21/01/2019
Bài 87 (Sách bài tập - tập 2 - trang 53)
21/01/2019
Bài 87 (Sách bài tập - tập 2 - trang 53)Cho góc xOy khác góc bẹt, điểm A thuộc cạnh Ox, điểm B thuộc cạnh Oy
a) Hãy tìm điểm M nằm trong góc xOy, cách đều Ox, Oy và cách đều A, B
b) Nếu OA = OB thì có bao nhiêu điểm M thỏa mãn các điều kiện trong câu a) ?
Theo dõi (0) 1 Trả lời -


Tìm số dư khi chia 2^2011chia cho 31
bởi minh dương
 21/01/2019
21/01/2019
tìm số dư khi chia 22011chia cho 31
Theo dõi (0) 1 Trả lời -


Tìm x,y
a . (x+ 4/ 2007)+ (x+3/2008)=(x+2/2009)+(x+1/2010)
b . 2x+1 . 3y-2 = 12x
Theo dõi (0) 1 Trả lời -


Tìm giá trị của biểu thức sau:
a/6a3-a10+4a3+a10-8a3+a với a=-2
b/4x6y3-3x6y3+2x2y2-x6y3-x2y2+y với x=1 ; y=-1
Theo dõi (0) 1 Trả lời -


Tìm Min của biểu thức A = ( 2x + 1/3)^4 - 1
bởi Hoa Lan
 21/01/2019
21/01/2019
a) Tìm Min của biểu thức A = ( 2x + 1/3)^4 - 1
b) Tìm Max của biểu thức B = -(4/9x - 2/15 ) ^ 6 + 3
Theo dõi (0) 1 Trả lời -


Tìm số a thỏa mãn a/3=b/5, 3a+b=2
bởi Thụy Mây
 21/01/2019
21/01/2019
tìm số a thỏa mãn a/3=b/5, 3a+b=2
Theo dõi (0) 1 Trả lời -


Tìm x biết (x-1)(x-3) < 0
bởi truc lam
 21/01/2019
21/01/2019
tìm x biết: a) (x-1)(x-3)<0
b)3x+x\(^2\)=0
Theo dõi (0) 1 Trả lời -


Tìm cặp số x,y tự nhiên 49-y^2=12{x-2001}^2
bởi Thanh Nguyên
 10/12/2019
10/12/2019
Tìm cặp số x,y tự nhiên sao cho: 49-y^2=12{x-2001}^2
Theo dõi (0) 1 Trả lời -


Tính \(P=\dfrac{1}{0,25}.\left(1\dfrac{1}{4}\right)^2+25.\left[\dfrac{1}{\left(\dfrac{4}{3}\right)^2}:\left(\dfrac{5}{4}\right)^3\right]:\dfrac{1}{\left(-\dfrac{2}{3}\right)^3}\)
Theo dõi (0) 1 Trả lời -


Tìm n sao cho (0,25)^n=1/256
bởi thanh hằng
 10/12/2019
10/12/2019
Tìm n sao cho \(\left(0,25\right)^n=\dfrac{1}{256}\)
Theo dõi (0) 1 Trả lời -


Tính (5^4-5^3)^3/125^5
bởi hi hi
 10/12/2019
10/12/2019
Tính:
a) \(\dfrac{\left(5^4-5^3\right)^3}{125^5}\)
b) \(\dfrac{9^3}{\left(3^4-3^3\right)^2}\)
Theo dõi (0) 1 Trả lời -


Tìm x, biết 2^(x+2).3^(x+1).5^x=10800
bởi Trần Bảo Việt
 11/12/2019
11/12/2019
Tìm x biết
2x+2 . 3x+1 . 5x = 10800
Theo dõi (0) 1 Trả lời -


Tìm số TN n thỏa mãn điều kiện: \(2.2^2+3.2^3+4.2^4+....+n.2^n=2^{n+11}\)
Theo dõi (0) 1 Trả lời -


Chứng minh (10^2006 +53)/9 là số tự nhiên
bởi Thanh Nguyên
 11/12/2019
11/12/2019
chung minh rang
a.(10^2006 +53)/9 la so tu nhien
b.-0,7 (43^43-17^17)la so nguyen
Theo dõi (0) 1 Trả lời -


Tính giá trị của biểu thức x^2013-2014.x^2012+2014.x^2011-2010+2014x-2014 khi x=2013
bởi Nguyễn Phương Khanh
 11/12/2019
11/12/2019
Tính giá trị của biểu thức:
\(x^{2013}-2014.x^{2012}+2014.x^{2011}-2010+2014.x-2014\) khi x= 2013
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 56 trang 18 SBT Toán 7 Tập 1
Bài tập 57 trang 18 SBT Toán 7 Tập 1
Bài tập 59 trang 18 SBT Toán 7 Tập 1
Bài tập 6.1 trang 18 SBT Toán 7 Tập 1
Bài tập 6.2 trang 18 SBT Toán 7 Tập 1
Bài tập 6.3 trang 18 SBT Toán 7 Tập 1
Bài tập 6.4 trang 18 SBT Toán 7 Tập 1
Bài tập 6.5 trang 19 SBT Toán 7 Tập 1
Bài tập 6.6 trang 19 SBT Toán 7 Tập 1





