Ôn tập Toán 12 Chương 2 Hàm Số Lũy Thừa, Hàm Số Mũ & Hàm Số Lôgarit
Các dạng toán liên quan đến Mũ và Lôgarit trong chương trình phổ thông chủ yếu đòi hỏi khả năng ghi nhớ công thức và vận dụng linh hoạt các phương pháp giải là có thể xử lý hầu hết các bài tập từ cơ bản đến nâng cao, không cần khả năng tư duy hay suy luận quá phức tạp. Tài liệu Ôn tập Toán 12 Chương 2 về Hàm số lũy thừa, Hàm số mũ và hàm số lôgarit sẽ giúp các em hệ thống hóa lại kiến thức đã học để ghi nhớ và vận dụng tốt hơn vào việc giải bài tập. Để ôn tập hiệu quả, các em có thể xem lại nội dung chi tiết của từng bài học, giải bài tập SGK và làm một số đề kiểm tra 1 tiết được HỌC247 biên soạn theo hình thức trắc nghiệm online. Ngoài ra, các em có thể tải các file đề kiểm tra về máy để tiện tham khảo và ôn tập. Chúc các em ôn tập tốt và đạt thành tích cao trong học tập.
Đề cương Ôn tập Toán 12 Chương 2
A. Tóm tắt lý thuyết
1. Công thức mũ và lũy thừa
Cho a và b > 0, m và n là những số thực tùy ý, ta có các công thức mũ và lũy thừa sau:
.png)
2. Công thức lôgarit
Cho a<0≠1,b>0 và x,y>0, ta có các công thức sau:
(1).png)
Công thức đổi cơ số:
.png)
3. Hàm số lũy thừa, hàm số mũ, hàm số lôgarit
a) Hàm số lũy thừa
Bảng tóm tắt các tính chất của hàm số lũy thừa y=xα trên khoảng (0;+∞)
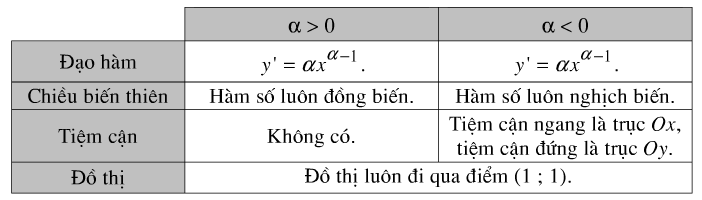
b) Hàm số mũ
Bảng tóm tắt các tính chất của hàm số mũ y=ax(a>0,a≠1)

c) Hàm số lôgarit
Bảng tóm tắt các tính chất của hàm số lôgarit y=logax(a>0,a≠1)

4. Đạo hàm của hàm số lũy thừa, hàm số mũ và hàm số lôgarit
.png)
5. Phương trình và bất phương trình mũ
Các phương pháp giải
- Phương pháp đưa về cùng cơ số.
- Phương pháp lôgarit hóa.
- Phương pháp đặt ẩn phụ.
- Phương pháp hàm số.
6. Phương trình và bất phương trình lôgarit
Các phương pháp giải
- Phương pháp đưa về cùng cơ số
- Phương pháp mũ hóa.
- Phương pháp đặt ẩn phụ.
- Phương pháp hàm số.
B. Bài tập minh họa
Bài 1: Cho a, b, c > 0; a, b, c ≠1 thỏa mãn ac = b2. CMR: logab+logcb=2logab.logcb.
Hướng dẫn giải
ac=b2⇒logb a+logb c=2⇒1loga b+1logc b=2
⇒logc b+loga bloga b.logc b=2⇒logc b+loga b=2loga b.logc b.
Bài 2: Cho log35=a. Tính log7545 theo a.
Hướng dẫn giải
log7545=log345log375=log3(32.5)log3(3.52)=log332+log35log33+log352=2+log351+2log35=2+a1+2a.
Bài 3: Một người gửi tiết kiệm ngân hàng với lãi suất 6,8%/năm và lãi hàng năm được nhập vào vốn. Cho biết số tiền cả gốc và lãi được tính theo công thức T=A(1+r)n, trong đó A là số tiền gửi, r là lãi suất và n là số kỳ hạn gửi. Hỏi sau bao nhiêu năm người đó thu được gấp đôi số tiền ban đầu?
Hướng dẫn giải
Sau n năm số tiền thu được là T=A(1+0,068)n
Để T = 2A thì phải có (1,068)n=2 (hay (1+6,8%)n=2)
⇔n=log1,068.2≈10,54
Vậy muốn thu được gấp đôi số tiền ban đầu, người đó phải gửi 11 năm.
Bài 4: Giải phương trình log88x2=3log28x.
Hướng dẫn giải
Điều kiện: {x>0log88x2≥0⇔0<x<2√2.
log88x2=3log28x⇔log88−log8x2=3.log28x
⇔3log28x+2log8x2−1=0
Đặt t=log8x, phương trình trở thành: 3t2+2t−1=0⇔[t=−1t=13
Với: t=−1⇔log8x=−1⇔x=18
Với: t=13⇔log8x=13⇔x=2
Vậy tập nghiệm phương trình là: {18;2}.
Bài 5: Giải bất phương trình: log0,5x+2log0,25(x−1)+log26≥0.
Hướng dẫn giải
Điều kiện: x > 1 (*).
Khi đó ta có:
log0,5x+2log0,25(x−1)+log26≥0
⇔log2x−log2(x−1)+log26≥0
⇔log2[x(x−1)]≤log26⇔x(x−1)≤6⇔x2−x−6≤0
⇔−2≤x≤3.
Kết hợp điều kiện (*) ta được 1<x≤3
Vậy tập nghiệm bất phương trình là S = (1;3].
Bài 6: Giải phương trình 27x−5.32−3x=4.
Hướng dẫn giải
27x−5.32−3x=4⇔27x−4527x=4⇔(27x)2−4.27x−45=0
Đặt: t=27x(t>0) ta được t2−4t−45=0⇔t=9 (Do t>0).
⇒33x=32⇔3x=2⇔x=23.
Vậy phương trình đã cho có nghiệm là x=23.
Bài 7: Giải bất phương trình 4x−3x>1.
Hướng dẫn giải
4x−3x>1⇔4x>3x+1⇔1>(34)x+(14)x
Với x≤1 ta có: (34)x⩾34(14)x⩾14⎫⎪
⎪
⎪⎬⎪
⎪
⎪⎭VP⩾1 Không thỏa mãn.
Với x>1 ta có: (34)x<34(14)x<14⎫⎪
⎪⎬⎪
⎪⎭VP<1 thỏa mãn.
Vậy bất phương trình có tập nghiệm là: S=(1;+∞).
Trắc nghiệm Toán 12 Chương 2
- Trắc nghiệm Toán 12 Chương 2 Bài 1
- Trắc nghiệm Toán 12 Chương 2 Bài 2
- Trắc nghiệm Toán 12 Chương 2 Bài 3
- Trắc nghiệm Toán 12 Chương 2 Bài 4
- Trắc nghiệm Toán 12 Chương 2 Bài 5
- Trắc nghiệm Toán 12 Chương 2 Bài 6
- Trắc nghiệm ôn tập Chương 2 Toán 12
Đề kiểm tra Toán 12 Chương 2
Đề kiểm tra trắc nghiệm online Chương 2 Toán 12 (Thi Online)
Phần này các em được làm trắc nghiệm online trong vòng 45 phút để kiểm tra năng lực và sau đó đối chiếu kết quả và xem đáp án chi tiết từng câu hỏi.
- 40 câu trắc nghiệm ôn tập Chương 2 Giải tích 12
- Trắc nghiệm Hàm số lũy thừa, hàm số mũ và hàm số logarit Giải tích 12 năm 2019
- Đề kiểm tra 1 tiết Chương 2 Giải tích 12 năm 2018 Trường THPT Đoàn Thượng
- Đề kiểm tra 1 tiết Chương 2 Giải tích 12 năm 2018 Trường THPT Ông Ích Khiêm
- Đề kiểm tra 1 tiết Chương 2 Giải tích 12 Trường THPT Lương Thế Vinh năm 2017 - 2018
- Đề kiểm tra 1 tiết chương 2 giải tích lớp 12 Trường THPT Thanh Hà năm 2017 - 2018
- Đề kiểm tra 1 tiết Chương 2 Giải tích 12 Trường THPT Ông Ích Khiêm năm 2017 - 2018
- Đề kiểm tra 1 tiết Chương 2 Giải tích 12 Trường THPT Đoàn Thượng năm 2017 - 2018
- 25 bài Trắc nghiệm Mũ và Logarit vận dụng cao Toán 12 năm học 2016 - 2017
Đề kiểm tra Chương 2 Toán 12 (Tải File)
Phần này các em có thể xem online hoặc tải file đề thi về tham khảo gồm đầy đủ câu hỏi và đáp án làm bài.
- Đề kiểm tra 1 tiết chương 2 giải tích 12 Trường THPT Đông Du năm học 2017 - 2018 có đáp án
- Đề kiểm tra 1 tiết Chương 2 giải tích 12 Trường THPT Thanh Hà năm 2017 có đáp án
- Đề kiểm tra 1 tiết Chương 2 Giải tích lớp 12 Trường THPT Nguyễn Trãi năm 2017 có đáp án
- Đề kiểm tra 1 tiết Chương 2 Giải tích lớp 12 trường THPT Ông Ích Khiêm năm 2017 có đáp án
- Đề kiểm tra 1 tiết chương 2 Giải tích 12 Trường THPT Huỳnh Mẫn Đạt năm 2017
- Đề kiểm tra 1 tiết Chương 2 giải tích 12 năm 2017 - Trường THPT An Hải
- Đề kiểm tra 1 tiết Chương 2 giải tích 12 năm 2017 - Trường THPT Đoàn Thượng có đáp án
- Đề kiểm tra 1 tiết chương 2 giải tích 12 Trường THPT Trần Quốc Tuấn năm học 2017 - 2018
- Đề kiểm tra 1 tiết chương 2 giải tích 12 Trường THPT Tôn Thất Tùng năm học 2017 - 2018
- 4 Đề kiểm tra 1 tiết môn Giải tích lớp 12 chương 2 năm 2016-2017 - THPT Đức Hoà
- 8 Đề kiểm tra 1 tiết môn Giải tích lớp 12 chương 2 năm 2016-2017 - THPT Nho Quan A
- 2 Đề kiểm tra 1 tiết môn Giải tích lớp 12 chương 2 năm 2016-2017 có đáp án
Lý thuyết từng bài Chương 2 và hướng dẫn giải bài tập SGK
Lý thuyết các bài học Toán 12 Chương 2
- Toán 12 Bài 1 Lũy thừa
- Toán 12 Bài 2 Hàm số lũy thừa
- Toán 12 Bài 3 Lôgarit
- Toán 12 Bài 4 Hàm số mũ Hàm số lôgarit
- Toán 12 Bài 5 Phương trình mũ và phương trình lôgarit
- Toán 12 Bài 6 Bất phương trình mũ và bất phương trình lôgarit
- Toán 12 Ôn tập chương 2 Hàm số lũy thừa, Hàm số mũ và Hàm số Lôgarit
Hướng dẫn giải bài tập Toán 12 Chương 2
- Giải bài tập Toán 12 Chương 2 Bài 1
- Giải bài tập Toán 12 Chương 2 Bài 2
- Giải bài tập Toán 12 Chương 2 Bài 3
- Giải bài tập Toán 12 Chương 2 Bài 4
- Giải bài tập Toán 12 Chương 2 Bài 5
- Giải bài tập Toán 12 Chương 2 Bài 6
- Giải bài ôn tập Chương 2 Toán 12
Để xem nội dung đầy đủ, chi tiết, các em đăng nhập vào tài khoản trên trang Hoc247.net. Trên mỗi tài liệu, Hoc247 đều hỗ trợ chức năng chia sẻ lên Facebook để giới thiệu bạn bè cùng vào học, tích lũy thêm điểm HP và có cơ hội nhận thêm nhiều phần quà có giá trị từ HỌC247! Chúc các em đạt kết quả thật cao.






