Giải bài 4 tr 39 sách SGK Toán lớp 9 Tập 1
Phát biểu và chứng minh định lí về mối liên hệ giữa phép nhân và phép khai phương. Cho ví dụ.
Hướng dẫn giải chi tiết
Phương pháp giải
Nếu \(x ≥ 0\) và \(x^2 = a\) thì \(x\) là căn bậc hai số học của số \(a\) không âm.
Lời giải chi tiết
Định lí: Nếu \(a \ge 0\) và \(b \ge 0\) thì \(\sqrt {ab} = \sqrt a .\sqrt b \)
Chứng minh: Vì \(a \ge 0,b \ge 0 \Rightarrow ab \ge 0,\) do đó \(\sqrt a ,\sqrt b ,\sqrt {ab} \) đều xác định
Ta có: \({\left( {\sqrt a .\sqrt b } \right)^2} = {\left( {\sqrt a } \right)^2}.{\left( {\sqrt b } \right)^2} = a.b\)
Do \(\sqrt a \ge 0,\sqrt b \ge 0 \Rightarrow \sqrt a .\sqrt b \ge 0\)
Vậy \(\sqrt a .\sqrt b \) là căn bậc hai số học của tích \(ab\)
Hay \(\sqrt a .\sqrt b = \sqrt {ab} \)
Ví dụ: \(\sqrt {49.36} = \sqrt {49} .\sqrt {36} \)\( = 7.6 = 42\)
-- Mod Toán 9 HỌC247
-
Cho biểu thức: \(\displaystyle Q = {a \over {\sqrt {{a^2} - {b^2}} }} - \left( {1 + {a \over {\sqrt {{a^2} - {b^2}} }}} \right):{b \over {a - \sqrt {{a^2} - {b^2}} }}\) với a > b > 0. Xác định giá trị của Q khi a = 3b
bởi Nguyễn Trà Giang
17/02/2021
Theo dõi (0) 1 Trả lời -
Rút gọn: \(\displaystyle Q = {a \over {\sqrt {{a^2} - {b^2}} }} - \left( {1 + {a \over {\sqrt {{a^2} - {b^2}} }}} \right):{b \over {a - \sqrt {{a^2} - {b^2}} }}\) với a > b > 0
bởi Anh Trần
17/02/2021
Theo dõi (0) 1 Trả lời -
Chứng minh đẳng thức sau: \(\displaystyle \left( {1 + {{a + \sqrt a } \over {\sqrt a + 1}}} \right)\left( {1 - {{a - \sqrt a } \over {\sqrt a - 1}}} \right) = 1 - a\) với a ≥ 0 và a ≠ 1
bởi hà trang
17/02/2021
Theo dõi (0) 1 Trả lời -
Chứng minh đẳng thức sau: \(\displaystyle {{a\sqrt b + b\sqrt a } \over {\sqrt {ab} }}:{1 \over {\sqrt a - \sqrt b }} = a - b\) với a, b dương và a ≠ b
bởi Lê Tấn Vũ
17/02/2021
Theo dõi (0) 1 Trả lời -
Chứng minh đẳng thức sau: \(\displaystyle \left( {{{\sqrt {14} - \sqrt 7 } \over {1 - \sqrt 2 }} + {{\sqrt {15} - \sqrt 5 } \over {1 - \sqrt 3 }}} \right):{1 \over {\sqrt 7 - \sqrt 5 }} = - 2\)
bởi An Vũ
17/02/2021
Theo dõi (0) 1 Trả lời -
Chứng minh đẳng thức sau: \(\displaystyle \left( {{{2\sqrt 3 - \sqrt 6 } \over {\sqrt 8 - 2}} - {{\sqrt {216} } \over 3}} \right).{1 \over {\sqrt 6 }} = - 1,5\)
bởi Hoàng My
17/02/2021
Theo dõi (0) 1 Trả lời -
Tìm x, biết: \(\displaystyle {5 \over 3}\sqrt {15{\rm{x}}} - \sqrt {15{\rm{x}}} - 2 = {1 \over 3}\sqrt {15{\rm{x}}} \)
bởi Nguyễn Tiểu Ly
17/02/2021
Theo dõi (0) 1 Trả lời -
Theo dõi (0) 1 Trả lời -
Rút gọn rồi tính giá trị của biểu thức sau: \(4{\rm{x}} - \sqrt {9{{\rm{x}}^2} + 6{\rm{x}} + 1} \) tại \(x= - \sqrt 3\)
bởi Phí Phương
17/02/2021
Theo dõi (0) 1 Trả lời -
Rút gọn rồi tính giá trị của biểu thức sau: \(\sqrt {1 - 10{\rm{a}} + 25{{\rm{a}}^2}} - 4{\rm{a}}\) tại \(a = \sqrt 2\)
bởi Tieu Giao
17/02/2021
Theo dõi (0) 1 Trả lời -
Rút gọn rồi tính giá trị của biểu thức sau: \(\displaystyle 1 + {{3m} \over {m - 2}}\sqrt {{m^2} - 4m + 4}\) tại \(m = 1,5\)
bởi thúy ngọc
17/02/2021
Theo dõi (0) 1 Trả lời -
Rút gọn rồi tính giá trị của biểu thức sau: \(\sqrt { - 9{\rm{a}}} - \sqrt {9 + 12{\rm{a}} + 4{{\rm{a}}^2}}\) tại \(a = - 9\)
bởi Phung Thuy
17/02/2021
Theo dõi (0) 1 Trả lời -
Phân tích thành nhân tử (với các số x, y, a, b không âm và a ≥ b): \(12 - \sqrt x - x\)
bởi Bo Bo
17/02/2021
Theo dõi (0) 1 Trả lời -
Phân tích thành nhân tử (với các số x, y, a, b không âm và a ≥ b): \(\sqrt {a + b} + \sqrt {{a^2} - {b^2}} \)
bởi Nguyễn Trọng Nhân
16/02/2021
Theo dõi (0) 1 Trả lời -
Phân tích thành nhân tử (với các số x, y, a, b không âm và a ≥ b): \(\sqrt {ax} - \sqrt {by} + \sqrt {bx} - \sqrt {ay} \)
bởi Nguyễn Minh Hải
17/02/2021
Theo dõi (0) 1 Trả lời -
Phân tích thành nhân tử (với các số x, y, a, b không âm và a ≥ b): \(xy - y\sqrt x + \sqrt x - 1\)
bởi hà trang
17/02/2021
Theo dõi (0) 1 Trả lời -
Rút gọn biểu thức sau: \(2\sqrt {{{\left( {\sqrt 2 - 3} \right)}^2}} + \sqrt {2.{{\left( { - 3} \right)}^2}} - 5\sqrt {{{\left( { - 1} \right)}^4}} \)
bởi Tra xanh
17/02/2021
Theo dõi (0) 1 Trả lời -
Rút gọn biểu thức sau: \(\displaystyle \left( {{1 \over 2}.\sqrt {{1 \over 2}} - {3 \over 2}.\sqrt 2 + {4 \over 5}.\sqrt {200} } \right):{1 \over 8}\)
bởi Nguyen Phuc
16/02/2021
Theo dõi (0) 1 Trả lời -
Rút gọn biểu thức sau: \(0,2\sqrt {{{\left( { - 10} \right)}^2}.3} + 2\sqrt {{{\left( {\sqrt 3 - \sqrt 5 } \right)}^2}} \)
bởi Nguyễn Tiểu Ly
17/02/2021
Theo dõi (0) 1 Trả lời -
Rút gọn biểu thức sau: \(\left( {\sqrt 8 - 3.\sqrt 2 + \sqrt {10} } \right)\sqrt 2 - \sqrt 5 \)
bởi Hồng Hạnh
17/02/2021
Theo dõi (0) 1 Trả lời -
Tìm giá trị biểu thức sau: \(\sqrt {21,6} .\sqrt {810.} \sqrt {{{11}^2} - {5^2}}\)
bởi Nguyen Dat
17/02/2021
Theo dõi (0) 1 Trả lời -
Tìm giá trị biểu thức sau: \(\displaystyle {{\sqrt {640} .\sqrt {34,3} } \over {\sqrt {567} }}\)
bởi Minh Tuyen
17/02/2021
Theo dõi (0) 1 Trả lời -
Tìm giá trị biểu thức sau: \(\displaystyle \sqrt {3{1 \over {16}}.2{{14} \over {25}}.2{{34} \over {81}}}\)
bởi Suong dem
16/02/2021
Theo dõi (0) 1 Trả lời -
Tìm giá trị biểu thức sau: \(\displaystyle \sqrt {{{25} \over {81}}.{{16} \over {49}}.{{196} \over 9}}\)
bởi Naru to
17/02/2021
Theo dõi (0) 1 Trả lời -
Phát biểu và chứng minh định lí về mối liên hệ giữa phép chia và phép khai phương. Cho ví dụ.
bởi Naru to
17/02/2021
Theo dõi (0) 1 Trả lời -
Phát biểu và chứng minh định lí về mối liên hệ giữa phép nhân và phép khai phương. Cho ví dụ.
bởi Mai Vàng
16/02/2021
Theo dõi (0) 1 Trả lời -
Theo dõi (0) 1 Trả lời -
Chứng minh \(\sqrt {a^2} = |a|\) với mọi số a.
bởi Hoang Vu
17/02/2021
Theo dõi (0) 1 Trả lời -
Theo dõi (0) 1 Trả lời
-
Hỏi đầu năm trường có bao nhiêu học sinh?
bởi Xoài Xoài
04/09/2020
Khối 9 của một trường đầu năm có số học sinh nam bằng số học sinh nữ. Đến hk2 thì số học sinh nam tăng 2 học sinh, số học sinh nữ tăng 8 học sinh, vì vậy số học sinh nữ chiếm 51 phần trăm tổng số học sinh của trường. Hỏi đầu năm trường có bao nhiêu học sinh?Theo dõi (0) 1 Trả lời -
Rút gọn \(P = (\frac{2\sqrt{x}}{\sqrt{x}+3} + \frac{\sqrt{x}}{\sqrt{x}-3} - \frac{3(\sqrt{x}+3)}{x-9}) : ( \frac{2\sqrt{x}-2}{\sqrt{x}-3} - 1)\)?
bởi Phạm Tuấn
03/09/2020
Cho \(P = (\frac{2\sqrt{x}}{\sqrt{x}+3} + \frac{\sqrt{x}}{\sqrt{x}-3} - \frac{3(\sqrt{x}+3)}{x-9}) : ( \frac{2\sqrt{x}-2}{\sqrt{x}-3} - 1)\)
a) Rút gọn Pb) Tìm x để P<-1
c) Tìm x < 4 nguyên để P có giá trị nguyên $\sqrt{x}$ = $\frac{\sqrt{3}+1}{\sqrt{2}}$
Theo dõi (0) 0 Trả lời -
Theo dõi (0) 0 Trả lời -
Chứng minh ({x^3} + {y^3} + {z^3} ge x + y + z)?
bởi Tiến Hưng
27/08/2020
Cho x, y, z>0 và xyz=1.Chứng minh \({x^3} + {y^3} + {z^3} \ge x + y + z\)
Mình cần gấp ạ!Theo dõi (0) 5 Trả lời -
Thu gọn biểu thức \(G = \left[ {\sqrt {1 + 2\sqrt {27\sqrt 2 + 1} } - \sqrt {5 - 3\sqrt 2 } } \right]:\sqrt {3\sqrt 2 - 4} \)?
bởi Thiên Ánh
13/08/2020
Thu gọn biết thức
G=[√(1+2√(27√2 +1)) - √(5-3√2)] : √(3√2 -4)
Mong mọi người giúp
Thanks
Theo dõi (0) 2 Trả lời -
Cho \(x^2+ y^2=1\). Chứng minh rằng: \(\sqrt {x^4-^x2 +y^2} +\sqrt{y^4-y^2 +x^2}=1\)?
bởi Lê Trần Minh Phương
28/07/2020
Cho x2 y2=1.CMR:căn(x4-x2 y2) căn(y4-y2 x2)=1
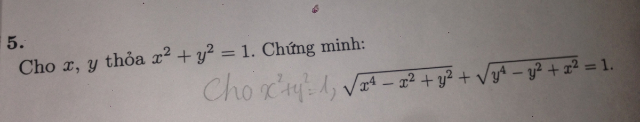Theo dõi (0) 2 Trả lời -
Giúpp ạ!!!
Theo dõi (0) 0 Trả lời -
Theo dõi (0) 0 Trả lời -
Giải phương trình x^2+4x+(√x^2-1)=2(√2x+3)-5?
bởi Nguyễn Thị Thu Hằng
01/07/2020
giải phương trình x^2+4x+(√x^2-1)=2(√2x+3)-5
Theo dõi (0) 8 Trả lời -
Tìm giá trị lớn nhất của biểu thức M?
bởi Ng H Trag
28/06/2020
giúp mk vs aj ! Thank kiuTheo dõi (0) 3 Trả lời -
Cho x, y, z khác 0 và x + y + z = 10. Tìm GTNN của \(\frac{1}{x} + \frac{1}{y} + \frac{1}{z}\)?
Giúp mình với ạ, tìm gg k ra :(Theo dõi (0) 0 Trả lời -
Rút gọn \(A = \left( {\frac{{\sqrt x }}{2} - \frac{1}{{\sqrt x }}} \right)\left( {\frac{{x - \sqrt x }}{{\sqrt x + 1}} - \frac{{x + \sqrt x }}{{\sqrt x + 1}}} \right)\?
bởi duong thuy
12/06/2020
Cho biểu thức A: (căn x/2 - 1/căn x)*(x - căn x/căn x+1-x+căn x/ căn x -1)
a, rút gọn A
b, tìm các giá trị x để A<-4
Theo dõi (0) 3 Trả lời -
Chứng minh \(\frac{1}{{{a^2} + {b^2} + {c^2}}} + \frac{{2021}}{{ab + bc + ca}} \ge 674\)?
bởi TÔ NGỌC BẢO LINH
07/06/2020
Chứng minh
\(\frac{1}{{{a^2} + {b^2} + {c^2}}} + \frac{{2021}}{{ab + bc + ca}} \ge 674\)
Theo dõi (0) 1 Trả lời -
Tính giá trị biểu thức \({B = {{\left( {\frac{{2 + \sqrt 3 }}{{\sqrt 2 + \sqrt {2 + \sqrt 3 } }}} \right)}^5} + {{\left( {\frac{{2 - \sqrt 3 }}{{\sqrt 2 - \sqrt {2 - \sqrt 3 } }}} \right)}^5}}\)
bởi Trịnh Lan Trinh
31/05/2020
Theo dõi (0) 1 Trả lời -
Rút gọn biểu thức
bởi Lê Gia Bảo
30/05/2020
\(A = \left( {\frac{{2x - 1 + \sqrt x }}{{1 - x}} + \frac{{2x\sqrt x + x - \sqrt x }}{{1 + x\sqrt x }}} \right).\frac{{\left( {x - \sqrt x } \right)\left( {1 - \sqrt x } \right)}}{{2\sqrt x - 1}} - 1\)
Theo dõi (0) 1 Trả lời -
Tìm giá trị của x để A = \(\frac{{3{x^3} - 14{x^2} + 3x + 36}}{{3{x^3} - 19{x^2} + 33x - 9}}\) có giá trị bằng 0
bởi Trần Hoàng Mai
29/05/2020
Theo dõi (0) 1 Trả lời -
Tìm giá trị của x để biểu thức A = \(\frac{{3{x^3} - 14{x^2} + 3x + 36}}{{3{x^3} - 19{x^2} + 33x - 9}}\) xác định
bởi Nguyễn Lệ Diễm
30/05/2020
Theo dõi (0) 1 Trả lời -
Tìm GTNN của \(A = \frac{{{x^2}}}{{x + y}} + \frac{{{y^2}}}{{y + z}} + \frac{{{z^2}}}{{z + x}}\) biết x, y, z > 0 ,\(\sqrt {xy} + \sqrt {yz} + \sqrt {zx} = 1.\)
bởi Mai Bảo Khánh
30/05/2020
Theo dõi (0) 1 Trả lời -
Rút gọn biểu thức \(A = \frac{{{x^2} - 2x}}{{{x^3} + 1}} + \frac{1}{2}.(\frac{1}{{1 + \sqrt {x + 2} }} + \frac{1}{{1 - \sqrt {x + 2} }})\)
bởi Lê Bảo An
30/05/2020
Theo dõi (0) 1 Trả lời -
Tìm điều kiện biểu thức \(A = \frac{{{x^2} - 2x}}{{{x^3} + 1}} + \frac{1}{2}.(\frac{1}{{1 + \sqrt {x + 2} }} + \frac{1}{{1 - \sqrt {x + 2} }})\) để A có nghĩa
bởi Trịnh Lan Trinh
30/05/2020
Theo dõi (0) 1 Trả lời -
Biết \(\sqrt 5 \) là số vô tỉ, hãy tìm các số nguyên a, b thỏa mãn: \(\frac{2}{{a + b\sqrt 5 }} - \frac{3}{{a - b\sqrt 5 }} = - 9 - 20\sqrt 5 \)
bởi Trần Hoàng Mai
30/05/2020
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Câu hỏi 2 trang 39 SGK Toán 9 Tập 1
Câu hỏi 3 trang 39 SGK Toán 9 Tập 1
Câu hỏi 5 trang 39 SGK Toán 9 Tập 1
Bài tập 70 trang 40 SGK Toán 9 Tập 1
Bài tập 71 trang 40 SGK Toán 9 Tập 1
Bài tập 72 trang 40 SGK Toán 9 Tập 1
Bài tập 73 trang 40 SGK Toán 9 Tập 1
Bài tập 74 trang 40 SGK Toán 9 Tập 1
Bài tập 75 trang 40 SGK Toán 9 Tập 1
Bài tập 76 trang 41 SGK Toán 9 Tập 1
Bài tập 96 trang 21 SBT Toán 9 Tập 1
Bài tập 97 trang 21 SBT Toán 9 Tập 1
Bài tập 98 trang 22 SBT Toán 9 Tập 1
Bài tập 99 trang 22 SBT Toán 9 Tập 1
Bài tập 100 trang 22 SBT Toán 9 Tập 1
Bài tập 101 trang 22 SBT Toán 9 Tập 1
Bài tập 102 trang 22 SBT Toán 9 Tập 1
Bài tập 103 trang 22 SBT Toán 9 Tập 1
Bài tập 104 trang 23 SBT Toán 9 Tập 1
Bài tập 105 trang 23 SBT Toán 9 Tập 1
Bài tập 106 trang 23 SBT Toán 9 Tập 1
Bài tập 107 trang 23 SBT Toán 9 Tập 1
