Bài tập 37 trang 71 SBT Toán 9 Tập 1
a) Cho các điểm M(-1; -2), N(-2; -4), P(2; -3), Q(3; -4,5). Tìm tọa độ của các điểm M’, N’, P’, Q’ lần lượt đối xứng với các điểm M, N, P, Q qua trục Ox.
b) Vẽ đồ thị của các hàm số sau trên cùng một hệ trục tọa độ:
y = |x|;
y = |x + 1|.
c) Tìm tọa độ giao điểm của đồ thị của các hàm số y = |x| và y = |x + 1|.
Từ đó, suy ra phương trình |x| = |x + 1| có nghiệm duy nhất.
Hướng dẫn giải chi tiết
a) (h.25)
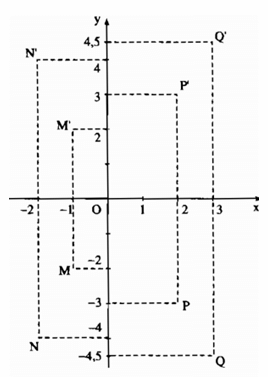
Gọi M’, N’, P’, Q’ là các điểm lần lượt đối xứng qua các điểm M, N, P, Q qua trục Ox, ta thấy rằng hoành độ của các điểm đối xứng nhau qua trục hoành bằng nhau, còn tung độ của các điểm đó thì đối nhau: M’(-1; 2); N’(-2; 4); P’(2; 3); Q’(3; 4,5).
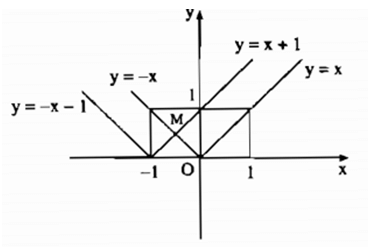
b) (h.26)
Ta vẽ đồ thị y = x với x ≥ 0.
Vẽ đồ thị y = -x với x ≤ 0.
Ta vẽ đồ thị y = x + 1 với x ≥ -1
Vẽ đồ thị y = -x – 1 với x ≤ -1.
c) (h.26) Đồ thị y = -x cắt đồ thị y = x + 1 tại điểm M(xo, yo). Vì M thuộc cả hai đồ thị nên tọa độ của M phải thỏa mãn các hàm số, nghĩa là:
Đồ thị y = |x| và đồ thị y = |x + 1| chỉ cắt nhau tại một điểm duy nhất M((-1)/2; 1/2).
Suy ra phương trình |x| = |x + 1| chỉ có nghiệm duy nhất x = (-1)/2.
-- Mod Toán 9 HỌC247
-


Cho A = \(1+2^1+2^2+2^3+...+2^{2018}\)
Lấy A chia cho 31 thì số dư là?
Theo dõi (0) 1 Trả lời -


Tìm m để y = ( 1 - 2m )x + m + 1 là hàm hằng
bởi hai trieu
 29/10/2018
29/10/2018
Cho y = ( 1 - 2m )x + m + 1. Tìm m để h/số y là hàm hằng.
Theo dõi (0) 1 Trả lời -


Tìm chữ số hàng trăm của tích 5009 . 8018. 2015. 2016
Theo dõi (0) 1 Trả lời -


Tìm giá trị lớn nhất của biểu thức A= căn(4x+2 cănx +1)+căn(4y+2 căny+1)+căn(4z+2 cănz +1)
bởi Mai Trang
 15/01/2019
15/01/2019
Cho các số x,y,z > 0 thỏa mãn x+y+z = 12 . Tìm gt lớn nhất của biểu thức :
A = \(\sqrt{4x+2\sqrt{x}+1}\) + \(\sqrt{4y+2\sqrt{y}+1}\) + \(\sqrt{4z+2\sqrt{z}+1}\)
Theo dõi (0) 1 Trả lời -


tìm nghiệm nguyên dương thỏa mãn
\(\left\{{}\begin{matrix}x+y+z=2\\3x^2+2y^2-z^2=13\end{matrix}\right.\)
Theo dõi (0) 1 Trả lời -


Tìm max của P=1/(2a+b+c)^2+1/(2b+c+a)^2+1/2c+a+b)^2
bởi Naru to
 16/01/2019
16/01/2019
cho 3 số thực dương a,b,c thay đổi thỏa mãn \(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}=3\)
tìm max của \(P=\dfrac{1}{\left(2a+b+c\right)^2}+\dfrac{1}{\left(2b+c+a\right)^2}+\dfrac{1}{\left(2c+a+b\right)^2}\)
Theo dõi (0) 1 Trả lời -


Giải bài toán sau:
1, \(\sqrt{48}\) +\(\sqrt{5\dfrac{1}{3}}\) + 2\(\sqrt{75}\) -5\(\sqrt{1\dfrac{1}{3}}\)
Theo dõi (0) 1 Trả lời -


voi gia tri nao cua m thi ham so bac nhat
a,y=(m-5)x+2dong bien
b,y=(2-m)x-3
Theo dõi (0) 1 Trả lời -


Tìm x, biết 4x^3 + 4x^4 - x2 - x = 0
bởi Nguyễn Thị Thu Huệ
 16/01/2019
16/01/2019
1, Tìm x, biết:
a, 4x3 + 4x4 - x2 - x = 0.
Theo dõi (0) 1 Trả lời -


Tìm giá trị lớn nhất của biểu thức P=(a-b)^2-2(a+b)
bởi Lê Viết Khánh
 16/01/2019
16/01/2019
cho a;b là các số thực thỏa mãn :\(a,b\in\left[\dfrac{1}{4}\overset{.}{,}2\right]\) và \(a+b=4ab\)
tìm giá trị lớn nhất của biểu thức : \(P=\left(a-b\right)^2-2\left(a+b\right)\)
thánh nào giúp giùm đi :((
@Akai Haruma , @Lightning Farron 2 bác làm giùm nha nếu đc
Theo dõi (0) 1 Trả lời -


Biết x/2=y/3=7, vậy 3x +2y =?
bởi Van Tho
 16/01/2019
16/01/2019
Biết \(\dfrac{x}{2}=\dfrac{y}{3}=7.\) Vậy 3x +2y =?
Theo dõi (0) 1 Trả lời -


Giá trị của biểu thức A= x3 + y3 + 3x2y +3xy2 với x + y = 5 thì A=?
Theo dõi (0) 1 Trả lời -


Tìm giá trị lớn nhất của biểu thức M=a^3+b^3+2000
bởi Nguyễn Hiền
 16/01/2019
16/01/2019
Cho a,b là 2 số thực thỏa mãn \(a^2+b^2=a+b+ab\). Tìm giá trị lớn nhất của biểu thức: \(M=a^3+b^3+2000\)
Theo dõi (0) 1 Trả lời -


Với x + y = 1 thì giá trị của biểu thức A = 2(x^3 + y^3) - 3(x^2 + y^2) + 30
bởi Đào Lê Hương Quỳnh
 16/01/2019
16/01/2019
Với x + y = 1 thì giá trị của biểu thức
A = 2(x3 + y3) - 3(x2 + y2) + 30
Theo dõi (0) 1 Trả lời -


Tìm các số nguyên x,y thoả mãn:
\(\left(y+2\right)x^{2017}-y^2-2y-1=0\)
Theo dõi (0) 1 Trả lời -


với n là số tự nhiên chứng minh rằng n(2n+7)(7n+1) chia hết cho 6
Theo dõi (0) 1 Trả lời -


Tìm các giá trị của m, biết đường thẳng d đi qua điểm A(-1, 2), Vẽ đồ thị hàm số với giá trị tìm được của m
bởi Mai Trang
 16/01/2019
16/01/2019
cho hàm số y = (m + 4)x - m + 6 có đồ thị là đường thẳng d
a) Tìm các giá trị của m, biết đường thẳng d đi qua điểm A(-1, 2), Vẽ đồ thị hs với giá trị tìm đc của m
b) Chứng minh với m thay đổi các đường thẳng d luôn đi qua 1 điểm cố định
Theo dõi (0) 1 Trả lời -


Chứng minh rằng:
\(\dfrac{1}{2\sqrt{1}}+\dfrac{1}{3\sqrt{2}}+....+\dfrac{1}{\left(n+1\right)\sqrt{n}}< 2\)
Theo dõi (0) 1 Trả lời -


Giá trị của biểu thức tan36-cot54 bằng bao nhiêu
bởi Mai Hoa
 16/01/2019
16/01/2019
Giá trị của biểu thức \(\tan36-\cot54\)bằng
Theo dõi (0) 1 Trả lời -


Chứng minh rằng căn(a^2/b)+căn(b^2/a) >= căn a + căn b
bởi Hong Van
 16/01/2019
16/01/2019
Chứng minh rằng:
\(\sqrt{\dfrac{a^2}{b}}+\sqrt{\dfrac{b^2}{a}}\ge\sqrt{a}+\sqrt{b}\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng mọi số thực khác không x,y ta có x^2/y^2 + y^2/x^2 +4 >= 3(x/y +y/x)
bởi Mai Bảo Khánh
 16/01/2019
16/01/2019
CMR mọi số thực khác không x,y ta có :
\(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}+4\ge3\left(\dfrac{x}{y}+\dfrac{y}{x}\right)\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng với mọi số thực x ta luôn có :
\(\left(2x+1\right)\sqrt{x^2-x+1}>\left(2x-1\right)\sqrt{x^2+x+1}\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng a^2+a+/ căn(a^2+a+1)>=2
bởi Nguyễn Thủy
 16/01/2019
16/01/2019
Chứng minh rằng:
\(\dfrac{a^2+a+2}{\sqrt{a^2+a+1}}\ge2\)
Theo dõi (0) 1 Trả lời -


câu 1 : tính giá trị bt : \(P=\left(1-\dfrac{1}{1+2}\right)\cdot\left(1-\dfrac{1}{1+2+3}\right)...\left(1-\dfrac{1}{1+2+...+2018}\right)\)
b) cho 2 số thực a, b lần lượt thoả mãn các hệ thức \(a^3-3a^2+5b+11=0\) chứng minh a+b=2
câu 2 : cho bt :
\(Q=\left(\dfrac{\sqrt{1+a}}{\sqrt{1+a}-\sqrt{1-a}}+\dfrac{1-a}{\sqrt{1-a^2}-1+a}\right)\cdot\left(\sqrt{\dfrac{1}{a^2}-1}-\dfrac{1}{a}\right)\cdot\sqrt{a^2-2a+1}\)
với 0<a<1
a) rút gọn Q
b) so sánh Q và \(Q^3\)
câu 3 : cho các số thực x,y thoả mãn \(\left(x+\sqrt{2018+x^2}\right)\cdot\left(y+\sqrt{2018+y^2}\right)=2018\)
tính gtbt \(Q=x^{2019}+y^{2019}+2018\cdot\left(x+y\right)+2020\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng xy/z^3(1+x)(1+y) + yz/x^3(1+y)(1+z) + zx/y^3(1+z)(1+x)>=1/16
bởi Phan Thiện Hải
 16/01/2019
16/01/2019
cho x,y,z là các số thực dương , thỏa mãn : xy+yz+zx=xyz
Chứng minh rằng \(\dfrac{xy}{z^3\left(1+x\right)\left(1+y\right)}+\dfrac{yz}{x^3\left(1+y\right)\left(1+z\right)}+\dfrac{zx}{y^3\left(1+z\right)\left(1+x\right)}\ge\dfrac{1}{16}\)Theo dõi (0) 1 Trả lời -


Chứng minh hàm số y=-2x+3 nghịch biến
bởi My Le
 29/10/2018
29/10/2018
Cho hàm số bậc nhất y=-2x+3
a) hàm số đã cho đồng biến hay nghịch biến trên R? Vì sao?
b) Gọi M là điểm có tọa độ (a;b) thuộc đồ thị nói trên. Xác định a;b biết rằng √a(√b +1)=2
Theo dõi (0) 1 Trả lời -


chứng minh rằng \(\sqrt{a^2+b^2}\ge\dfrac{a+b}{\sqrt{2}}\)với mọi a;b lớn hơn hoặc bằng 0
Theo dõi (0) 1 Trả lời -


Chứng minh bất đẳng thức:
\(a^2+b^2+c^2+d^2\ge a\left(b+c+d\right)\)
Ai giúp mình với
Theo dõi (0) 1 Trả lời -


Chứng minh bất đẳng thức a^2+b^2+c^2+d^2>= a(b+c+d)
bởi Goc pho
 16/01/2019
16/01/2019
Chứng minh bất đẳng thức:
\(a^2+b^2+c^2+d^2\ge a\left(b+c+d\right)\)
Ai giúp mình với ( đề chuẩn k sai nha )
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 35 trang 70 SBT Toán 9 Tập 1
Bài tập 36 trang 70 SBT Toán 9 Tập 1
Bài tập 38 trang 71 SBT Toán 9 Tập 1
Câu hỏi 1 trang 59 SGK Toán 9 Tập 1
Câu hỏi 2 trang 60 SGK Toán 9 Tập 1
Câu hỏi 32 trang 61 SGK Toán 9 Tập 1
Câu hỏi 33 trang 61 SGK Toán 9 Tập 1
Câu hỏi 34 trang 61 SGK Toán 9 Tập 1
Câu hỏi 35 trang 61 SGK Toán 9 Tập 1
Câu hỏi 36 trang 61 SGK Toán 9 Tập 1