Giải bài 2.17 tr 91 SBT Hình học 10
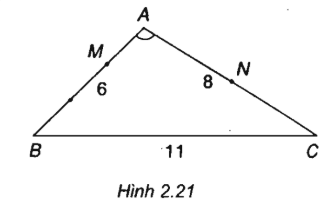
Tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 11 cm.
a) Tính \(\overrightarrow {AB} .\overrightarrow {AC} \) và chứng tỏ rằng tam giác ABC có góc A tù.
b) Trên cạnh AB lấy điểm M sao cho AM = 2 cm và gọi N là trung điểm của cạnh AC. Tính \(\overrightarrow {AM} .\overrightarrow {AN}\)
Hướng dẫn giải chi tiết
a)
\(\begin{array}{l}
\overrightarrow {AB} .\overrightarrow {AC} = \frac{1}{2}\left( {A{C^2} + A{B^2} - B{C^2}} \right) = \frac{1}{2}\left( {{8^2} + {6^2} - {{11}^2}} \right) = - \frac{{21}}{2}\\
= AB.AC.\cos A = - \frac{{21}}{2}
\end{array}\)
Suy ra góc A tù.
b) Ta có \(\overrightarrow {AM} = \frac{1}{3}\overrightarrow {AB} ,\overrightarrow {AN} = \frac{1}{2}\overrightarrow {AC} \)
Do đó \(\overrightarrow {AM} .\overrightarrow {AN} = \frac{1}{3}\overrightarrow {AB} .\frac{1}{2}\overrightarrow {AC} = \frac{1}{6}\overrightarrow {AB} .\overrightarrow {AC} = \frac{1}{6}.\left( { - \frac{{21}}{2}} \right) = - \frac{7}{4}\)
-- Mod Toán 10 HỌC247
-


Trong mặt phẳng Oxy, cho tam giác ABC có \(A = ( - 1;1),B = (1;3)\) và \(C = (1; - 1)\). Chứng minh tam giác ABC là tam giác vuông cân tại A.
bởi Lan Anh
 21/02/2021
Theo dõi (0) 1 Trả lời
21/02/2021
Theo dõi (0) 1 Trả lời -


Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau và cắt nhau tại M. Gọi P là trung điểm của cạnh AD. Chứng minh rằng MP vuông góc với BC khi và chỉ khi \(\overrightarrow {MA} .\overrightarrow {MC} = \overrightarrow {MB} .\overrightarrow {MD} \).
bởi Nguyễn Vũ Khúc
 21/02/2021
Theo dõi (0) 1 Trả lời
21/02/2021
Theo dõi (0) 1 Trả lời -


Cho tam giác đều ABC cạnh a. Tính \(\overrightarrow {AB} .\overrightarrow {AC} \) và \(\overrightarrow {AB} .\overrightarrow {BC} \).
bởi Tuấn Tú
 21/02/2021
Theo dõi (0) 1 Trả lời
21/02/2021
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC. Gọi H là trực tâm của tam giác và M là trung điểm của cạnh BC. Chứng minh rằng \(\overrightarrow {MH} .\overrightarrow {MA} = \dfrac{1}{4}B{C^2}\).
bởi hai trieu
 21/02/2021
Theo dõi (0) 1 Trả lời
21/02/2021
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2.15 trang 91 SBT Hình học 10
Bài tập 2.16 trang 91 SBT Hình học 10
Bài tập 2.18 trang 92 SBT Hình học 10
Bài tập 2.19 trang 92 SBT Hình học 10
Bài tập 2.20 trang 92 SBT Hình học 10
Bài tập 2.21 trang 92 SBT Hình học 10
Bài tập 2.22 trang 92 SBT Hình học 10
Bài tập 2.23 trang 92 SBT Hình học 10
Bài tập 2.24 trang 92 SBT Hình học 10
Bài tập 2.25 trang 92 SBT Hình học 10
Bài tập 2.26 trang 92 SBT Hình học 10
Bài tập 2.27 trang 92 SBT Hình học 10
Bài tập 2.28 trang 92 SBT Hình học 10
Bài tập 4 trang 51 SGK Hình học 10 NC
Bài tập 5 trang 51 SGK Hình học 10 NC
Bài tập 6 trang 51 SGK Hình học 10 NC
Bài tập 7 trang 52 SGK Hình học 10 NC
Bài tập 8 trang 52 SGK Hình học 10 NC
Bài tập 9 trang 52 SGK Hình học 10 NC
Bài tập 10 trang 52 SGK Hình học 10 NC
Bài tập 11 trang 52 SGK Hình học 10 NC
Bài tập 12 trang 52 SGK Hình học 10 NC