Giải bài 2.23 tr 92 SBT Hình học 10
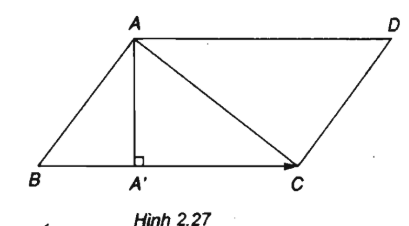
Trong mặt phẳng Oxy cho tam giác ABC với A = (2;4), B = (- 3;1) và C = (3;1). Tính:
a) Tọa độ điểm D để tứ giác ABCD là hình bình hành;
b) Tọa độ chân của đường cao vẽ từ đỉnh A.
Hướng dẫn giải chi tiết
a) Vì ABCD là hình bình hành nên ta có:
\(\overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \left\{ \begin{array}{l}
{x_B} - {x_A} = {x_C} - {x_D}\\
{y_B} - {y_A} = {y_C} - {y_D}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{x_D} = {x_C} - \left( {{x_B} - {x_A}} \right) = 8\\
{y_D} = {y_C} - \left( {{y_B} - {y_A}} \right) = 4
\end{array} \right.\)
Vậy D(8;4).
b) Gọi A(x;y) là chân đường cao vẽ từ A ta có:
\(\overrightarrow {AA'} \bot \overrightarrow {BC} \) hay \(\overrightarrow {AA'} .\overrightarrow {BC} = \overrightarrow 0 \) và \(\overrightarrow {BA'} \) cùng phương với \(\overrightarrow {BC} \).với \(\overrightarrow {AA'} = \left( {x - 2;y - 4} \right);\overrightarrow {BC} = \left( {6; - 2} \right),\overrightarrow {BA'} = \left( {x + 3;y - 1} \right)\)
Do đó:
\(\begin{array}{l}
\Leftrightarrow \left\{ \begin{array}{l}
\left( {x - 2} \right).6 + \left( {y - 4} \right).\left( { - 2} \right) = 0\\
- 2\left( {x + 3} \right) = 6\left( {y - 1} \right) = 0
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
6x - 12 - 2y + 8 = 0\\
- 2x - 6 - 6y + 6 = 0
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
6x - 2y - 4 = 0\\
- 2x - 6y = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{x_{A'}} = \frac{3}{5}\\
{y_{A'}} = - \frac{1}{5}
\end{array} \right.
\end{array}\)
-- Mod Toán 10 HỌC247
-


CM: Tam giác ABC vuông tại A
bởi Trần Trung Hiếu
 02/01/2021
02/01/2021
Cho tam giác ABC với A (4;1) B (1;3) C(6;4)
a CM: tam giác abc vuông tại A
b, tính S của tam giác abc
Theo dõi (0) 0 Trả lời -


Góc giữa hai vectơ là bao nhiêu?
bởi Nguyễn Hèn
 14/04/2020
14/04/2020
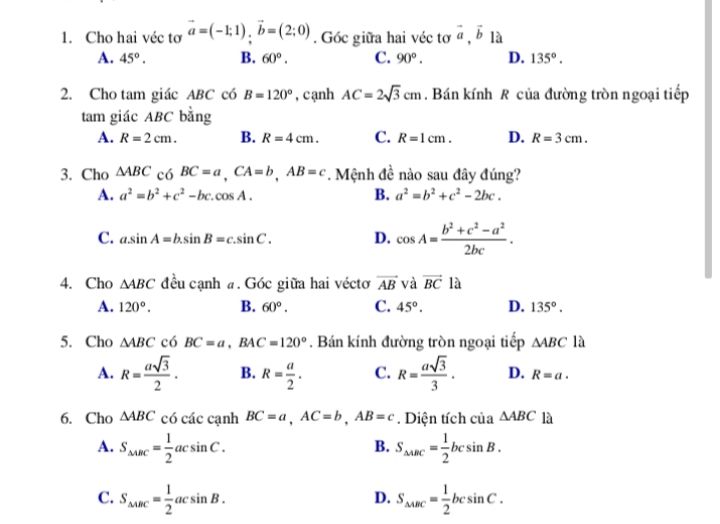 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giá trị của m để \(\overrightarrow a ;\,\,\overrightarrow b \) cùng phương?
bởi Lương Thị Huyền Trang
 09/04/2020
09/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm tọa độ điểm D thỏa đẳng thức vectơ
bởi Minh Tưởng
 16/03/2020
Giải giúp mk câu nayd vs
16/03/2020
Giải giúp mk câu nayd vs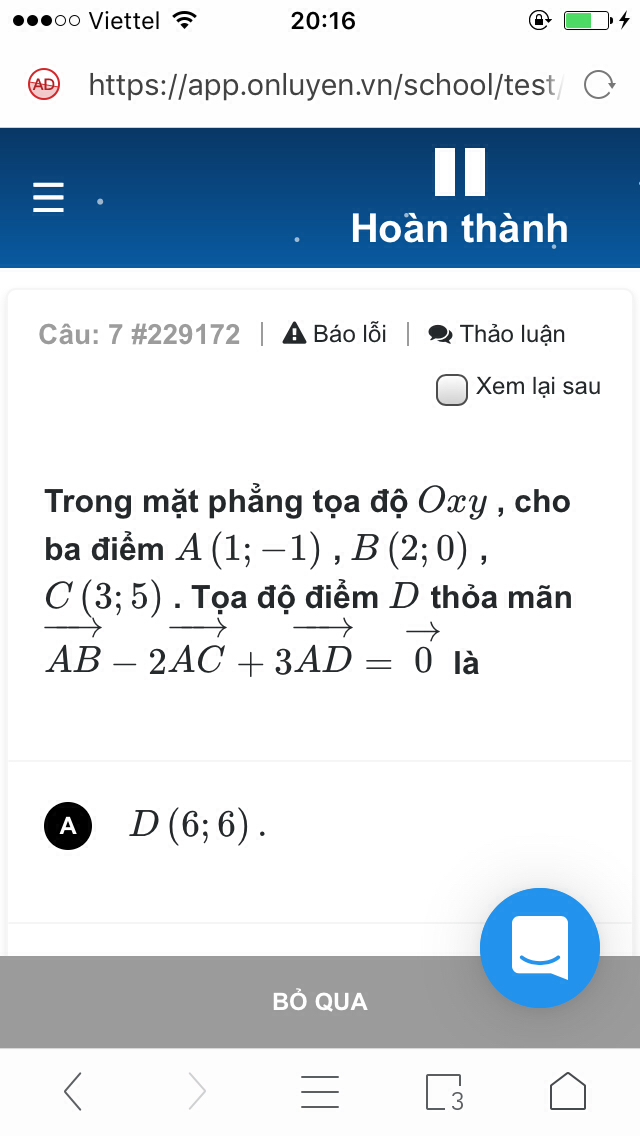 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2.21 trang 92 SBT Hình học 10
Bài tập 2.22 trang 92 SBT Hình học 10
Bài tập 2.24 trang 92 SBT Hình học 10
Bài tập 2.25 trang 92 SBT Hình học 10
Bài tập 2.26 trang 92 SBT Hình học 10
Bài tập 2.27 trang 92 SBT Hình học 10
Bài tập 2.28 trang 92 SBT Hình học 10
Bài tập 4 trang 51 SGK Hình học 10 NC
Bài tập 5 trang 51 SGK Hình học 10 NC
Bài tập 6 trang 51 SGK Hình học 10 NC
Bài tập 7 trang 52 SGK Hình học 10 NC
Bài tập 8 trang 52 SGK Hình học 10 NC
Bài tập 9 trang 52 SGK Hình học 10 NC
Bài tập 10 trang 52 SGK Hình học 10 NC
Bài tập 11 trang 52 SGK Hình học 10 NC
Bài tập 12 trang 52 SGK Hình học 10 NC