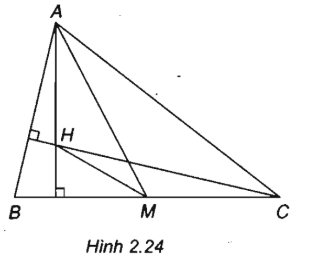
Giải bài 2.20 tr 92 SBT Hình học 10
Cho tam giác ABC. Gọi H là trực tâm của tam giác và M là trung điểm của cạnh BC. Chứng minh rằng \(\overrightarrow {MH} .\overrightarrow {MA} = \frac{1}{4}B{C^2}\).
Hướng dẫn giải chi tiết
\(\begin{array}{l}
\overrightarrow {HM} = \frac{1}{2}\left( {\overrightarrow {HB} + \overrightarrow {HC} } \right)\\
\Rightarrow \overrightarrow {AM} .\overrightarrow {HM} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\left( {\overrightarrow {HB} + \overrightarrow {HC} } \right)\\
= \frac{1}{4}\left( {\overrightarrow {AB} .\overrightarrow {HB} + \underbrace {\overrightarrow {AB} .\overrightarrow {HC} }_{ = 0} + \underbrace {\overrightarrow {AC} .\overrightarrow {HB} }_{ = 0} + \overrightarrow {AC} .\overrightarrow {HC} } \right)\\
= \frac{1}{4}\left( {\overrightarrow {AB} .\overrightarrow {HB} + \overrightarrow {AC} .\overrightarrow {HC} } \right)\\
= \frac{1}{4}\left[ {\overrightarrow {AB} \left( {\overrightarrow {HC} + \overrightarrow {CB} } \right) + \overrightarrow {AC} .\left( {\overrightarrow {HB} + \overrightarrow {BC} } \right)} \right]\\
= \frac{1}{4}\left[ {\underbrace {\overrightarrow {AB} .\overrightarrow {HC} }_{ = 0} + \overrightarrow {AB} .\overrightarrow {CB} + \underbrace {\overrightarrow {AC} .\overrightarrow {HB} }_{ = 0} + \overrightarrow {AC} .\overrightarrow {BC} } \right]\\
= \frac{1}{4}\left( {\overrightarrow {AB} .\overrightarrow {HC} + \overrightarrow {AC} .\overrightarrow {BC} } \right) = \frac{1}{4}\left( {\overrightarrow {AB} .\overrightarrow {CB} - \overrightarrow {AC} .\overrightarrow {CB} } \right)\\
= \frac{1}{4}\overrightarrow {CB} .\left( {\underbrace {\overrightarrow {AB} - \overrightarrow {AC} }_{\overrightarrow {CB} }} \right) = \frac{1}{4}{\overrightarrow {CB} ^2} = \frac{1}{4}{\overrightarrow {BC} ^2}
\end{array}\)
-- Mod Toán 10 HỌC247
-


Cho hai vec tơ \(\overrightarrow a \) và \(\overrightarrow b \) đều khác véc tơ \(\overrightarrow 0 \). Tích vô hướng \(\overrightarrow a .\overrightarrow b \) khi nào dương, khi nào âm và khi nào bằng \(0\)?
bởi Sam sung
 21/02/2021
Theo dõi (0) 1 Trả lời
21/02/2021
Theo dõi (0) 1 Trả lời -


Trên mặt phẳng \(Oxy\) cho điểm \(A(-2; 1)\). Gọi \(B\) là điểm đối xứng với điểm \(A\) qua gốc tọa độ \(O\). Tìm tọa độ của điểm \(C\) có tung độ bằng \(2\) sao cho tam giác \(ABC\) vuông ở \(C\).
bởi hi hi
 19/02/2021
Theo dõi (0) 1 Trả lời
19/02/2021
Theo dõi (0) 1 Trả lời -


Trên mặt phẳng tọa độ \(Oxy\) cho bốn điểm: \(A(7; -3); B(8; 4); C(1; 5); D(0;-2)\). Chứng minh rằng tứ giác \(ABCD\) là hình vuông.
bởi Hương Lan
 20/02/2021
Theo dõi (0) 1 Trả lời
20/02/2021
Theo dõi (0) 1 Trả lời -


Trên mặt phẳng Oxy hãy tính góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) trong trường hợp sau: \(\overrightarrow a = (-2; -2\sqrt3)\), \(\overrightarrow b = (3; \sqrt3)\)
bởi trang lan
 20/02/2021
Theo dõi (0) 1 Trả lời
20/02/2021
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2.18 trang 92 SBT Hình học 10
Bài tập 2.19 trang 92 SBT Hình học 10
Bài tập 2.21 trang 92 SBT Hình học 10
Bài tập 2.22 trang 92 SBT Hình học 10
Bài tập 2.23 trang 92 SBT Hình học 10
Bài tập 2.24 trang 92 SBT Hình học 10
Bài tập 2.25 trang 92 SBT Hình học 10
Bài tập 2.26 trang 92 SBT Hình học 10
Bài tập 2.27 trang 92 SBT Hình học 10
Bài tập 2.28 trang 92 SBT Hình học 10
Bài tập 4 trang 51 SGK Hình học 10 NC
Bài tập 5 trang 51 SGK Hình học 10 NC
Bài tập 6 trang 51 SGK Hình học 10 NC
Bài tập 7 trang 52 SGK Hình học 10 NC
Bài tập 8 trang 52 SGK Hình học 10 NC
Bài tập 9 trang 52 SGK Hình học 10 NC
Bài tập 10 trang 52 SGK Hình học 10 NC
Bài tập 11 trang 52 SGK Hình học 10 NC
Bài tập 12 trang 52 SGK Hình học 10 NC