Bài tập 10 trang 52 SGK Hình học 10 NC

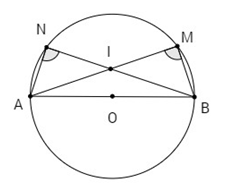
a) Ta có: 

\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {AM} .\overrightarrow {AI}  = \left( {\overrightarrow {AB}  + \overrightarrow {BM} } \right).\overrightarrow {AI} \\
 = \overrightarrow {AB} .\overrightarrow {AI}  + \overrightarrow {BM} .\overrightarrow {AI} \\
 = \overrightarrow {AB} .\overrightarrow {AI} \left( {do\overrightarrow {BM} .\overrightarrow {AI}  = 0} \right)
\end{array}\\
\begin{array}{l}
\overrightarrow {BN} .\overrightarrow {BI}  = \left( {\overrightarrow {BA}  + \overrightarrow {AN} } \right).\overrightarrow {BI} \\
 = \overrightarrow {BA} .\overrightarrow {BI}  + \overrightarrow {AN} .\overrightarrow {BI} \\
 = \overrightarrow {BA} .\overrightarrow {BI} \left( {do\overrightarrow {AN} .\overrightarrow {BI}  = 0} \right)
\end{array}
\end{array}\)

b) Theo câu a), ta có:

\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {AM} .\overrightarrow {AI}  + \overrightarrow {BN} .\overrightarrow {BI} \\
 = \overrightarrow {AB} .\overrightarrow {AI}  + \overrightarrow {BA} .\overrightarrow {BI} 
\end{array}\\
\begin{array}{l}
 = \overrightarrow {AB} \left( {\overrightarrow {AI}  - \overrightarrow {BI} } \right)\\
 = \overrightarrow {AB} .\overrightarrow {AB}  = A{B^2} = 4{R^2}
\end{array}
\end{array}\)

-- Mod Toán 10 HỌC247