Giải bài 2.19 tr 92 SBT Hình học 10
Cho hai véctơ \(\overrightarrow a \) và \(\overrightarrow b \) có \(\left| {\overrightarrow a } \right| = 5,\left| {\overrightarrow b } \right| = 12\) và \(\left| {\overrightarrow a + \overrightarrow b } \right| = 13\). Tính tích vô hướng \(\overrightarrow a \left( {\overrightarrow a + \overrightarrow b } \right)\) và suy ra góc giữa hai vec tơ \(\overrightarrow a \) và \({\overrightarrow a + \overrightarrow b }\).
Hướng dẫn giải chi tiết
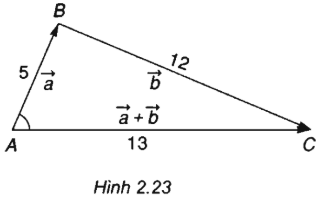
Dựng tam giác ABC có AB = 5, BC= 12 và AC = 13.
Ta có \(\overrightarrow b \) có \(\left| {\overrightarrow a } \right| = 5,\left| {\overrightarrow b } \right| = 12\) và \(\left| {\overrightarrow a + \overrightarrow b } \right| = 13\) và \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow a + \overrightarrow b \).
Khi đó \(\vec a\left( {\vec a + \vec b} \right) = \overrightarrow {AB} .\overrightarrow {AC} \)
Mặt khác ta có:
\(\begin{array}{l}
\overrightarrow {AB} .\overrightarrow {AC} = \frac{1}{2}\left( {A{C^2} + A{B^2} - B{C^2}} \right)\\
= \frac{1}{2}\left( {{{13}^2} + {5^2} - {{12}^2}} \right) = 25
\end{array}\)
Suy ra \(\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} = \frac{{25}}{{5.13}} \approx 0,3846\)
-- Mod Toán 10 HỌC247
-


Tam giác ABC vuông tại A và có \(AB = AC = a\). Tính: \(\overrightarrow {AB} .\overrightarrow {AC} \).
bởi Bao Chau
 21/02/2021
Theo dõi (0) 1 Trả lời
21/02/2021
Theo dõi (0) 1 Trả lời -


Chứng minh: \((\overrightarrow a + \overrightarrow b )(\overrightarrow a - \overrightarrow b ) = {\left| {\overrightarrow a } \right|^2} - {\left| {\overrightarrow b } \right|^2}\)
bởi Ha Ku
 22/02/2021
Theo dõi (0) 1 Trả lời
22/02/2021
Theo dõi (0) 1 Trả lời -


Chứng minh: \({(\overrightarrow a - \overrightarrow b )^2} = {\left| {\overrightarrow a } \right|^2} + {\left| {\overrightarrow b } \right|^2} - 2\overrightarrow a .\overrightarrow b \)
bởi Nguyễn Xuân Ngạn
 22/02/2021
Theo dõi (0) 1 Trả lời
22/02/2021
Theo dõi (0) 1 Trả lời -


Chứng minh: \({(\overrightarrow a + \overrightarrow b )^2} = {\left| {\overrightarrow a } \right|^2} + {\left| {\overrightarrow b } \right|^2} + 2\overrightarrow a .\overrightarrow b \).
bởi Tay Thu
 21/02/2021
Theo dõi (0) 1 Trả lời
21/02/2021
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2.17 trang 91 SBT Hình học 10
Bài tập 2.18 trang 92 SBT Hình học 10
Bài tập 2.20 trang 92 SBT Hình học 10
Bài tập 2.21 trang 92 SBT Hình học 10
Bài tập 2.22 trang 92 SBT Hình học 10
Bài tập 2.23 trang 92 SBT Hình học 10
Bài tập 2.24 trang 92 SBT Hình học 10
Bài tập 2.25 trang 92 SBT Hình học 10
Bài tập 2.26 trang 92 SBT Hình học 10
Bài tập 2.27 trang 92 SBT Hình học 10
Bài tập 2.28 trang 92 SBT Hình học 10
Bài tập 4 trang 51 SGK Hình học 10 NC
Bài tập 5 trang 51 SGK Hình học 10 NC
Bài tập 6 trang 51 SGK Hình học 10 NC
Bài tập 7 trang 52 SGK Hình học 10 NC
Bài tập 8 trang 52 SGK Hình học 10 NC
Bài tập 9 trang 52 SGK Hình học 10 NC
Bài tập 10 trang 52 SGK Hình học 10 NC
Bài tập 11 trang 52 SGK Hình học 10 NC
Bài tập 12 trang 52 SGK Hình học 10 NC