Bài tập 12 trang 52 SGK Hình học 10 NC
Cho đoạn thẳng AB cố định, AB = 2a và một số k2. Tìm tập hợp các điểm M sao cho MA2−MB2 = k2
Hướng dẫn giải chi tiết
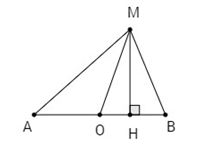
Gọi O là trung điểm đoạn AB, H là hình chiếu của MM lên AB. Ta có:
\(\begin{array}{l}
M{A^2} - M{B^2} = {k^2} \Leftrightarrow {\overrightarrow {MA} ^2} - {\overrightarrow {MB} ^2} = {k^2}\\
\Leftrightarrow \left( {\overrightarrow {MA} + \overrightarrow {MB} } \right).\left( {\overrightarrow {MA} - \overrightarrow {MB} } \right) = {k^2}\\
\Leftrightarrow 2\overrightarrow {MO} .\overrightarrow {BA} = {k^2}\\
\Leftrightarrow 2\left( {\overrightarrow {MH} + \overrightarrow {HO} } \right).\overrightarrow {BA} = {k^2}\\
\Leftrightarrow 2\overrightarrow {HO} .\overrightarrow {BA} = {k^2}\left( {do\overrightarrow {MH} .\overrightarrow {BA} = 0} \right)
\end{array}\)
Suy ra H cố định nằm trên tia OB
Và \(OH = \frac{{{k^2}}}{{4a}}\)
Do H là hình chiếu của M lên AB nên tập hợp các điểm M là đường thẳng vuông góc với AB tại H, H nằm trên tia OB sao cho \(OH = \frac{{{k^2}}}{{4a}}\).
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





