Giải bài 2.24 tr 92 SBT Hình học 10
Trong mặt phẳng Oxy, cho tam giác ABC có A = (-1; 1), B = (1; 3) và C = (1; -1)
Chứng minh tam giác ABC là tam giác vuông cân tại A.
Hướng dẫn giải chi tiết
Ta có : \(\overrightarrow {AB} = \left( {2;2} \right),\overrightarrow {AC} = \left( {2; - 2} \right) \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = 2.2 + 2.\left( { - 2} \right) = 0\)
Mặt khác: \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {AC} } \right| = \sqrt {4 + 4} = 2\sqrt 2 \)
Vậy tam giác ABC vuông cân tại A.
-- Mod Toán 10 HỌC247
-


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho hai vecto a và vecto b thỏa mãn |a ⃗ |=2;|b ⃗ |=3;|a ⃗+b ⃗ |=4. Hãy tính A=(a ⃗-3b ⃗ )(2a ⃗+b ⃗ )
bởi VT Quỳnh
 03/03/2020
Giúp mình bài 3 với
03/03/2020
Giúp mình bài 3 với Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


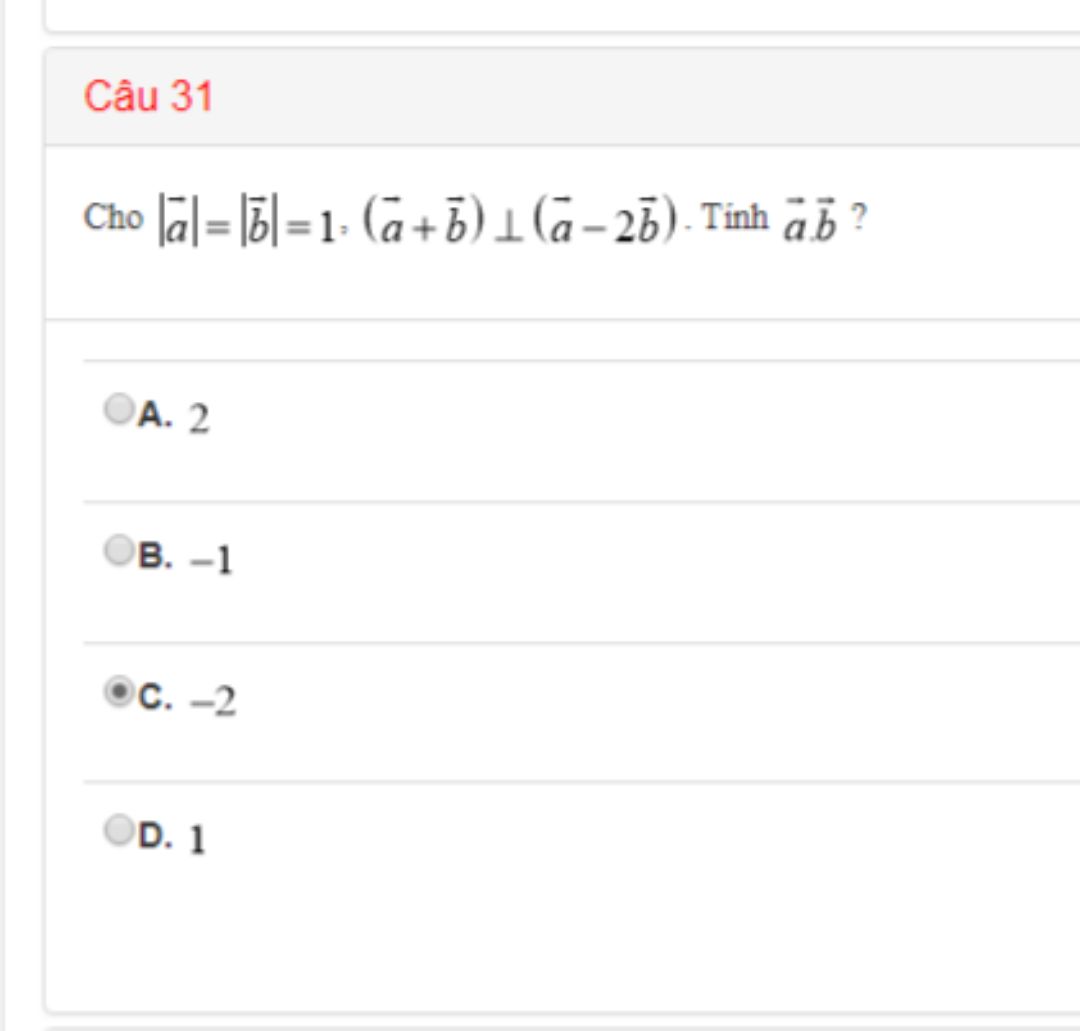
Tính vecto a.vecto b biết |a|=|b|=1
bởi Tiêu Lý Thanh Thanh
 28/02/2020
28/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 2.22 trang 92 SBT Hình học 10
Bài tập 2.23 trang 92 SBT Hình học 10
Bài tập 2.25 trang 92 SBT Hình học 10
Bài tập 2.26 trang 92 SBT Hình học 10
Bài tập 2.27 trang 92 SBT Hình học 10
Bài tập 2.28 trang 92 SBT Hình học 10
Bài tập 4 trang 51 SGK Hình học 10 NC
Bài tập 5 trang 51 SGK Hình học 10 NC
Bài tập 6 trang 51 SGK Hình học 10 NC
Bài tập 7 trang 52 SGK Hình học 10 NC
Bài tập 8 trang 52 SGK Hình học 10 NC
Bài tập 9 trang 52 SGK Hình học 10 NC
Bài tập 10 trang 52 SGK Hình học 10 NC
Bài tập 11 trang 52 SGK Hình học 10 NC
Bài tập 12 trang 52 SGK Hình học 10 NC





