Bài tập 6 trang 51 SGK Hình học 10 NC

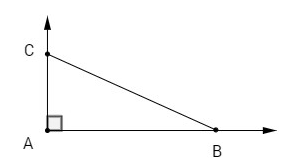
a) Ta có

\(\begin{array}{l}
\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = {150^0};\left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = {30^0};\\
\left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = {120^0}
\end{array}\)

Suy ra 

\(\begin{array}{*{20}{l}}
{\cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) + \sin \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) + \tan \frac{{\left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right)}}{2}}\\
\begin{array}{l}
 = \cos {150^0} + \sin {30^0} + \tan {60^0}\\
 =  - \frac{{\sqrt 3 }}{2} + \frac{1}{2} + \sqrt 3  = \frac{{\sqrt 3  + 1}}{2}
\end{array}
\end{array}\)

b) Ta có \(\left( {\overrightarrow {CA} ,\overrightarrow {BA} } \right) = {90^0}\), do đó:

\(\begin{array}{*{20}{l}}
{\sin \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) + \cos \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right) + \cos \left( {\overrightarrow {CA} ,\overrightarrow {BA} } \right)}\\
\begin{array}{l}
 = \sin {90^0} + \cos {30^0} + \cos {90^0}\\
 = 1 + \frac{{\sqrt 3 }}{2} + 0 = \frac{{2 + \sqrt 3 }}{2}
\end{array}
\end{array}\)

-- Mod Toán 10 HỌC247