Hình học 9 Bài 6: Tính chất của hai tiếp tuyến cắt nhau

Định lý: 

Nếu hai tiếp tuyến của đường tròn cắt nhau tại 1 điểm thì:

• Điểm đó cách đều hai tiếp điểm
• Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến
• Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm

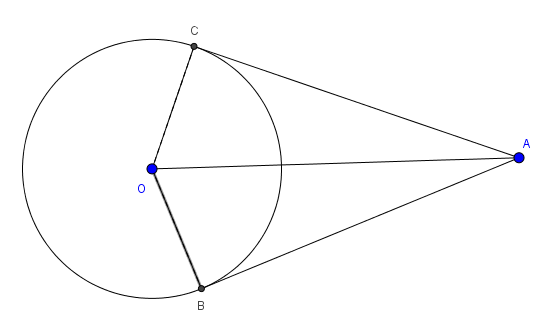
- Góc tạo bởi hai tiếp tuyến AB và AC là góc BAC

- Góc tạo bởi hai bán kính đi qua các tiếp điểm là BOC

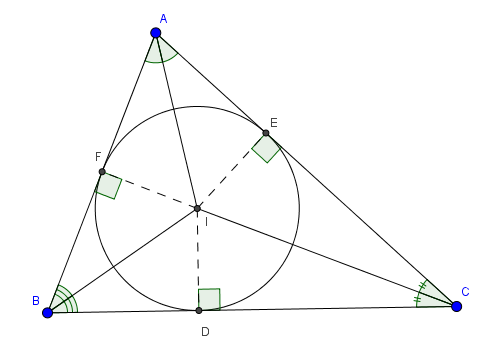
• Đường tròn tiếp xúc với 3 cạnh một tam giác gọi là đường tròn nội tiếp tam giác, còn tam giác gọi là ngoại tiếp đường tròn.
• Tâm của đường tròn nội tiếp tam giác là giao của các đường phân giác trong của tam giác đó

3. Đường tròn bàng tiếp tam giác

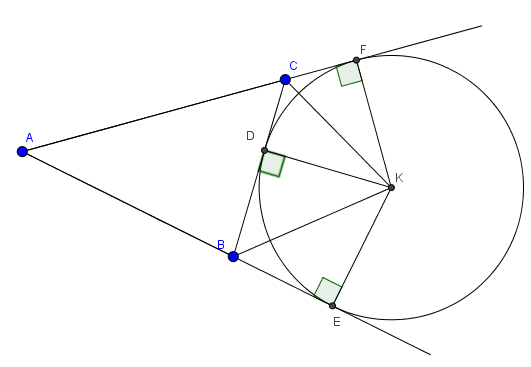
• Đường tròn tiếp xúc với một cạnh của một tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia gọi là đường tròn bàng tiếp tam giác.

( Hình trên gọi là Đường tròn bàng tiếp trong góc A của tam giác ABC)

• Tâm của đường tròn bàng tiếp trong góc A là giao điểm của hai đường phân giác ngoài các góc B và C hoặc là giao điểm của đường phân giác trong góc A với phân giác ngoài góc B (hoặc C).
• Với một tam giác có 3 đường tròn bàng tiếp tam giác

Bài 1: Cho (O) từ M ngoài đường tròn kẻ hai tiếp tuyến MA, MB của (O). Trên tia OB lấy C sao cho OB=BC. CMR: \(\widehat{BMC}=\frac{1}{2}.\widehat{BMA}\)

Hướng dẫn:

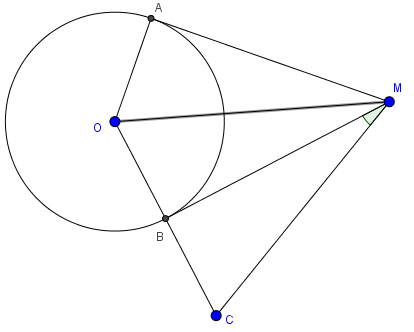
Ta có: MO là tia phân giác góc AMB nên \(\widehat{OMB}=\frac{1}{2}.\widehat{BMA}\)

Xét tam giác OMC có OB vừa là đường cao vừa là trung tuyến nên tam giác MOC cân tại M suy ra MB là phân giác góc OMC

\(\Rightarrow \widehat{BMC}=\widehat{OMB}=\frac{1}{2}.\widehat{BMA}\)

Bài 2: Cho đường tròn (O;R) và một điểm A ở ngoài đường tròn. Vẽ các tiếp tuyến AB, AC. CMR: \(\widehat{BAC}=60^{\circ}\Leftrightarrow OA=2R\)

Hướng dẫn: 

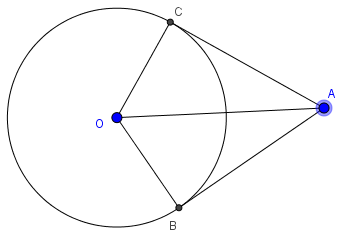
 \(\widehat{BAC}=60^o\Leftrightarrow \widehat{OAB}=30^o\Leftrightarrow sin \widehat{OAB}=\frac{1}{2}=\frac{OB}{OA}=\frac{R}{OA}\Leftrightarrow OA=2R\)

Bài 3: Chứng minh rằng diện tích tam giác ngoại tiếp một đường tròn được tính theo công thức: S=pr, Trong đó p là nửa chu vi tam giác, r là bán kính đường tròn nội tiếp

Hướng dẫn:

\(S_{ABC}=S_{AOB}+S_{BOC}+S_{AOC}=\frac{1}{2}.(AB+BC+AC).r=p.r\)

Bài 1: Cho nửa đường tròn tâm O đường kính AB. Vẽ các tia Ax vuông góc AB, By vuông góc với AB ở cùng phía với nửa đường tròn. I là một điểm trên nửa đường tròn đó. Tiếp tuyến tại I cắt Ax, By lần lượt tại C, D.

a) CMR: Tam giác COD là tam giác vuông 

b) Tim vị trí điểm I để chu vi tứ giác ACDB là nhỏ nhất. Tính chu vi đó theo R

Hướng dẫn:

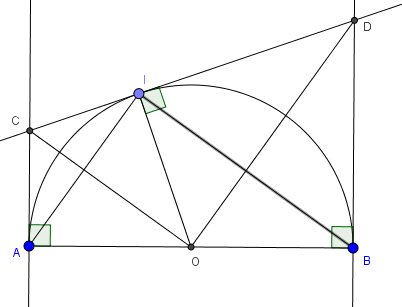
a) Ta có tam giác IAB vuông tại I 

Gọi E là giao điểm của AI và CO, F là giao điểm của IB và OD. Xét tứ giác IEOF có 3 góc vuông nên IEOF là hình chữ nhật suy ra \(\widehat{EOF}=90^{\circ}\Rightarrow \Delta COD\) vuông tại O

b) Vì tiếp tuyến tại A và I cắt nhau tại C nên CA=CI, tương tự DI=DB \(\Rightarrow AC+BD=CD\). Ta lại có \(CD\geq AB\) vì AB là đoạn vuông góc của 2 đường song song là AC và BD 

Khi đó: \(2P_{ACDB}=AC+BD+CD+AB=2CD+AB\geq 3.AB=3R\)

Bài 2: Cho tam giác ABC cân tại A nội tiếp đường tròn (O) . Các tiếp tuyến của (O) vẽ từ A và C cắt nhau tại M. Trên tia AM lấy D sao cho AD=BC. CMR: AC, BD, OM đồng quy

Hướng dẫn:

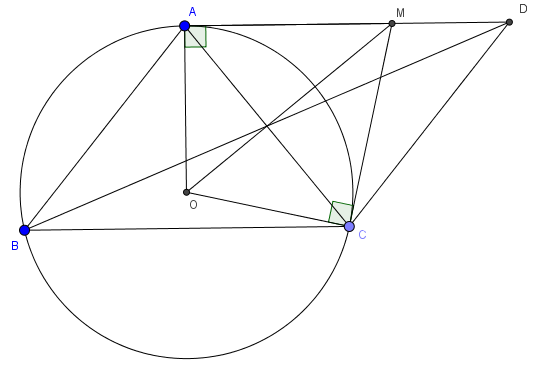
• Trước tiên ta sẽ chứng minh ABCD là hình bình hành

Ta có AO vuông góc BC, AO vuông góc AD nên \(AD\parallel BC\), mà AD=BC nên ABCD là hình bình hành

Gọi E là giao điểm của AC và OM. theo tính chất hai tiếp tuyến cắt nhau thì E là trung điểm AC (do tam giác MAC cân tại M, có ME đường cao)

Do ABCD là hình bình hành nên đường chéo sẽ qua trong điểm mỗi đường. Vậy BD đi qua E

Qua bài giảng Tính chất của hai tiếp tuyến cắt nhau này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như : 

• Tính chất hai tiếp tuyến cắt nhau
• Đường tròn nội tiếp tam giác

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Hình học 9 Bài 6 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Cho đường tròn (O). M là điểm ngoài đường tròn, vẽ hai tiếp tuyến MA, MB của (O). Khẳng định nào sau đây là sai

  • A. \(MA=MB\)
  • B. \(OM\perp AB\)
  • C. \(\widehat{OMA}=\widehat{OMB}\)
  • D. \(OM=2.AB\)

• Câu 2:

  Phát biểu nào sau đây là đúng

  • A. Có 3 đường tròn nội tiếp một tam giác
  • B. Có chỉ một đường tròn bàng tiếp một tam giác
  • C. Giao điểm của các đường phân giác trong chính là tâm đường tròn bàng tiếp tam giác đó
  • D. giao điểm của phân giác trong góc A và phân giác ngoài tại B là tâm đường tròn bầng tiếp trong góc A

Câu 3-5: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Hình học 9 Bài 6 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Toán 9 tập 1

Bài tập 26 trang 115 SGK Toán 9 Tập 1

Bài tập 27 trang 115 SGK Toán 9 Tập 1

Bài tập 28 trang 116 SGK Toán 9 Tập 1

Bài tập 29 trang 116 SGK Toán 9 Tập 1

Bài tập 30 trang 116 SGK Toán 9 Tập 1

Bài tập 31 trang 116 SGK Toán 9 Tập 1

Bài tập 32 trang 116 SGK Toán 9 Tập 1

Bài tập 48 trang 164 SBT Toán 9 Tập 1

Bài tập 49 trang 164 SBT Toán 9 Tập 1

Bài tập 50 trang 164 SBT Toán 9 Tập 1

Bài tập 51 trang 164 SBT Toán 9 Tập 1

Bài tập 52 trang 165 SBT Toán 9 Tập 1

Bài tập 53 trang 165 SBT Toán 9 Tập 1

Bài tập 54 trang 165 SBT Toán 9 Tập 1

Bài tập 55 trang 165 SBT Toán 9 Tập 1

Bài tập 56 trang 165 SBT Toán 9 Tập 1

Bài tập 57 trang 165 SBT Toán 9 Tập 1

Bài tập 58 trang 165 SBT Toán 9 Tập 1

Bài tập 59 trang 165 SBT Toán 9 Tập 1

Bài tập 60 trang 166 SBT Toán 9 Tập 1

Bài tập 61 trang 166 SBT Toán 9 Tập 1

Bài tập 62 trang 166 SBT Toán 9 Tập 1

Bài tập 63 trang 166 SBT Toán 9 Tập 1

Bài tập 6.1 trang 166 SBT Toán 9 Tập 1

Bài tập 6.2 trang 167 SBT Toán 9 Tập 1

Bài tập 6.3 trang 167 SBT Toán 9 Tập 1

Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HỌC247 sẽ sớm trả lời cho các em.