Bài tập 56 trang 165 SBT Toán 9 Tập 1

Hướng dẫn giải

Sử dụng kiến thức: 

\(*\)) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.

\(*\)) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

Lời giải chi tiết

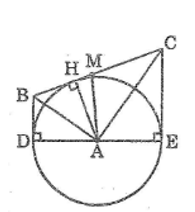
\(a)\) Theo tính chất hai tiếp tuyến cắt nhau ta có:

+ \(AB\) là tia phân giác của góc \(HAD\)  

Suy ra: \(\widehat {DAB} = \widehat {BAH}\)

+ \(AC\) là tia phân giác của góc \(HAE\)

Suy ra: \(\widehat {HAC} = \widehat {CAE}\)

Ta có: \(\widehat {HAD} + \widehat {HAE} = 2(\widehat {BAH} + \widehat {HAC})\)\( = 2.\widehat {BAC} = 2.90^\circ  = 180^\circ \)

Vậy ba điểm \(D, A, E\) thẳng hàng.

\(b)\) Gọi \(M\) là trung điểm của \(BC\)

Theo tính chất của tiếp tuyến, ta có: \(AD \bot BD;AE \bot CE\)

Suy ra: \(BD // CE\)

Vậy tứ giác \(BDEC\) là hình thang.

Vì \(M\) là trung điểm của \(BC\) và \(A\) là trung điểm của \(DE\) (vì DE là đường kính đường tròn (A))

Nên \(MA\) là đường trung bình của hình thang \(BDEC\)

Suy ra: \(MA // BD  \Rightarrow MA \bot DE\) (vì \(BD\bot DE\))

Trong tam giác vuông \(ABC\) có AM là đường trung tuyến nên ta có: \(MA = MB = MC=\dfrac{BC}2\)

Suy ra \(M\) là tâm đường tròn đường kính \(BC\) với \(MA\) là bán kính

Vậy \(DE\) là tiếp tuyến của đường tròn tâm \(M\) đường kính \(BC.\)

-- Mod Toán 9 HỌC247