Bài tập 58 trang 165 SBT Toán 9 Tập 1

Hướng dẫn giải

Sử dụng kiến thức:

+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

+) Tứ giác có ba góc vuông là hình chữ nhật.

+) Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

+) Định lí Py-ta-go: trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

+) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì điểm đó cách đều hai tiếp điểm.

Lời giải chi tiết

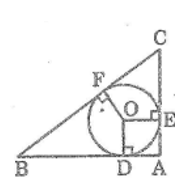
Vì đường tròn \((O)\) nội tiếp tam giác \(ABC\) nên AB, BC, AC là các tiếp tuyến của đường tròn. 

Gọi F là tiếp điểm của đường tròn (O) với tiếp tuyến BC.

\(a)\) Ta có: \(OD  \bot AB \Rightarrow \widehat {ODA} = 90^\circ \)

\(OE \bot AC \Rightarrow \widehat {OEA} = 90^\circ \)

\(\widehat {BAC} = 90^\circ \) (gt)

Tứ giác \(ADOE\) có ba góc vuông nên nó là hình chữ nhật

Lại có: \(AD = AE\) (tính chất hai tiếp tuyến cắt nhau)

Vậy tứ giác \(ADOE\) là hình vuông.

\(b)\) Áp dụng định lí Pi-ta-go vào tam giác vuông \(ABC\) ta có:

\(B{C^2} = A{B^2} + A{C^2} = {3^2} + {4^2} = 25\)

Suy ra: \( BC = 5 (cm)\)

Theo tính chất tiếp tuyến cắt nhau ta có:

\(AD = AE\)

\(      BD = BF\)

\(   CE = CF\)

Mà: \( AD = AB – BD\)

\(  AE = AC – CE\)

Suy ra:    \(AD + AE = AB – BD + (AC – CE )\)

\(  = AB + AC – (BD + CE )\)

\( = AB + AC – (BF + CF )\)

\( = AB + AC – BC\)

Suy ra:    \( AD = AE =\displaystyle {{AB + AC - BC} \over 2}\)\( = \displaystyle {{3 + 4 - 5} \over 2} = 1 (cm)\)

Vì tứ giác \(ADOE\) là hình vuông nên  \(OD=DA=1cm\)

Vậy bán kính của đường tròn \((O)\) là \(1cm.\)

-- Mod Toán 9 HỌC247