Giải bài 62 tr 166 sách BT Toán lớp 9 Tập 1
Cho nửa đường tròn tâm \(O\) có đường kính \(AB.\) Vẽ các tiếp tuyến \(Ax, By\) \((Ax, By\) và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ \(AB).\) Qua một điểm \(M\) thuộc nửa hình tròn, kẻ tiếp tuyến thứ ba cắt \(Ax,\) \(By\) theo thứ tự ở \(C, D.\) Gọi \(N\) là giao điểm của \(AD\) và \(BC, H\) là giao điểm của \(MN\) và \(AB.\) Chứng minh rằng:
\(a)\) \(MN ⊥ AB;\)
\(b)\) \(MN = NH.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng kiến thức:
+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
+) Sử dụng hệ quả định lí Ta-lét: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
+) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì điểm đó cách đều hai tiếp điểm.
+) Sử dụng định lí Ta-lét đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Lời giải chi tiết
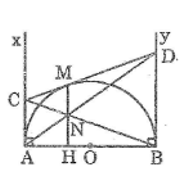
\(a)\) Theo tính chất tiếp tuyến, ta có:
\(Ax ⊥ AB\)
\(By ⊥ AB\)
Suy ra: \(Ax // By\) hay \(AC // BD\)
Trong tam giác \(BND,\) ta có: \(AC // BD\)
Suy ra: \(\displaystyle{{ND} \over {NA}} = {{BD} \over {AC}}\) (Hệ quả định lí Ta-lét) \((1)\)
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
\(AC = CM\) và \(BD = DM \;\; (2)\)
Từ \((1)\) và \((2)\) suy ra: \(\displaystyle{{ND} \over {NA}} = {{MD} \over {MC}}\)
Trong tam giác \(ACD,\) ta có: \(\displaystyle{{ND} \over {NA}} = {{MD} \over {MC}}\)
Suy ra: \(MN // AC\) ( Theo định lí đảo định lí Ta-lét)
Mà: \(AC ⊥ AB\) \((\)vì \(Ax ⊥ AB)\)
Suy ra: \(MN ⊥ AB\)
\(b)\) Trong tam giác \(ACD,\) ta có: \(MN // AC\)
Suy ra: \(\displaystyle{{MN} \over {AC}} = {{DN} \over {DA}}\) (Hệ quả định lí Ta-lét) \((3)\)
Trong tam giác \(ABC,\) ta có: \(NH // AC\) ( vì \(M, N, H\) thẳng hàng)
Suy ra: \(\displaystyle{{HN} \over {AC}} = {{BN} \over {BC}}\) (Hệ quả định lí Ta-lét) \((4)\)
Trong tam giác \(BDN,\) ta có: \(AC // BD\)
Suy ra: \(\displaystyle{{ND} \over {NA}} = {{BN} \over {NC}}\) (Hệ quả định lí Ta-lét)
\(\displaystyle \Rightarrow {{ND} \over {DN + NA}} = {{BN} \over {BN + NC}}\)
\(\displaystyle \Leftrightarrow {{ND} \over {DA}} = {{BN} \over {BC}}\) \((5)\)
Từ \((3), (4)\) và \((5)\) suy ra: \(\displaystyle{{MN} \over {AC}} = {{HN} \over {AC}} \Rightarrow MN = HN\).
-- Mod Toán 9 HỌC247
-


Bài 48 trang 164 sách bài tập toán 9 tập 1
bởi Lê Nhật Minh
 26/09/2018
Bài 48 (Sách bài tập - tập 1 - trang 164)
26/09/2018
Bài 48 (Sách bài tập - tập 1 - trang 164)Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AM, AN với đường tròn (M, N là các tiếp điểm)
a) Chứng minh rằng \(OA\perp MN\)
b) Vẽ đường kính NOC. Chứng minh rằng MC // AO
c) Tính độ dài các cạnh của tam giác AMN biết OM = 3cm, OA = 5cm
Theo dõi (0) 1 Trả lời -


Chứng minh rằng ΔKBC≈ΔOBE
bởi hi hi
 30/01/2019
30/01/2019
Cho (O) ,điểm K nằm bên ngoài (O) .Kẻ các tiếp tuyến KA,KB với (O) , ( A,B là các tiếp điểm ).Kẽ đk A,O,C, tiếp tuyến của (O) tại C cắt AB ở E. CMR:
a) \(\Delta KBC\approx\Delta OBE\)
b) \(CK\perp OE\)
Theo dõi (0) 1 Trả lời -


cho (O;R) có đường kính BC, lấy điểm A thuộc đường tròn tâm O sao cho AB=R
a. CM: tam giác ABC vuông và tính AC theo R
b. tiếp tuyến tại A của (O) cắt đường thẳng BC tại M. trên đường ròn tâm O lấy điểm D sao cho MD=MA( điểm D khác điểm A) , CMR: MD là tiếp tuyến của đường tròn tâm O
c. vẽ đường kính AK của (O) , MK cắt (O) tại E,( E khác K) . gọi H là giao điểm của AD và MO. CMR: ME.MK=MH.MO
Theo dõi (0) 1 Trả lời





