Bài tập 52 trang 165 SBT Toán 9 Tập 1

Hướng dẫn giải

Sử dụng kiến thức: Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì điểm đó cách đều hai tiếp điểm.

Lời giải chi tiết

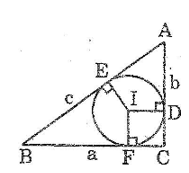
Gọi \(F\) là tiếp điểm của đường tròn \((I)\) với \(BC.\)

Theo tính chất của hai tiếp tuyến cắt nhau, ta có:

\(AE = AD\)

\(   BE = BF\)

\( CD = CF\)

Mà: \(AE = AB – BE\)

\( AD = AC – CD\)

Nên: \(AE + AD = (AB –BE) + (AC – CD)\)

\(   = AB + AC – (BE + CD)\)

\(   = AB + AC – (BF + CF) \)

\( = AB + AC – BC\)

Suy ra: \(AE + AD = c + b – a\)

Hay:  \(AE = AD =\displaystyle {{c + b - a} \over 2}\)

-- Mod Toán 9 HỌC247