Bài tập 61 trang 166 SBT Toán 9 Tập 1

Hướng dẫn giải

Sử dụng kiến thức:

\(*\)) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

\(*\)) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì

+)  Điểm đó cách đều hai tiếp điểm.

+) Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.

\(*\)) Sử dụng hệ thức lượng trong tam giác, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.

Lời giải chi tiết

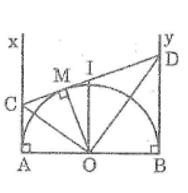
\(a)\) Theo tính chất tiếp tuyến, ta có:

\(Ax ⊥ AB\)

\(By ⊥ AB\)

Suy ra: \(Ax // By\) hay \(AC // BD\)

Suy ra tứ giác \(ABDC\) là hình thang

Gọi \(I\) là trung điểm của \(CD\)

Khi đó \(OI\) là đường trung bình của hình thang \(ABDC\)

Suy ra: \(OI // AC ⇒ OI ⊥ AB\) tại O

Vì \(OC\) và \(OD\) lần lượt là phân giác của \(\widehat {AOM}\) và \(\widehat {BOM}\) (tính chất hai tiếp tuyến cắt nhau) mà \(\widehat {AOM}\) và \(\widehat {BOM}\) là hai góc kề bù nên \(OC ⊥ OD\) ( tính chất hai góc kề bù) \( \Rightarrow \widehat {COD} = 90^\circ \)

Xét tam giác COD vuông tại O có OI là trung tuyến

Suy ra: \(\displaystyle IC = ID = IO = {1 \over 2}CD\) ( tính chất tam giác vuông)

Suy ra \(I\) là tâm đường tròn đường kính \(CD.\) Khi đó \(O\) nằm trên đường tròn tâm \(I\) đường kính \(CD\) và \(IO\) vuông góc với \(AB\) tại \(O.\)

Vậy đường tròn có đường kính \(CD\) tiếp xúc với \(AB\) tại \(O.\)

\(b)\) Theo tính chất hai tiếp tuyến cắt nhau, ta có:

\(CA = CM\)

\(BD = DM\)

Suy ra: \(AC + BD = CM + DM = CD\)

Chu vi hình thang \(ABDC\) bằng:

\(AB + BD + DC + CA = AB + 2CD\)

Vì đường kính \(AB\) của \((O)\) không thay đổi nên chu vi hình thang nhỏ nhất khi \(CD\) nhỏ nhất.

Ta có: \(CD ≥ AB\) nên \(CD\) nhỏ nhất khi và chỉ khi \(CD = AB\)

Khi đó \(CD // AB ⇔ OM ⊥ AB\) 

Vậy khi \(M\) là giao điểm của đường thẳng vuông góc với \(AB\) tại \(O\) với nửa đường tròn \((O)\) thì hình thang \(ABDC\) có chu vi nhỏ nhất.

\(c)\) Chu vi hình thang \(ABDC\) bằng: \(AB + 2CD\) (chứng minh trên)

Suy ra: \(14 = 4 + 2.CD ⇒ CD = 5 (cm)\)

Hay \(CM + DM = 5 \)\(⇒ DM = 5 – CM    \;  (1)\)

Tam giác \(COD\) vuông tại \(O\) có \(OM ⊥ CD\)

Theo hệ thức lượng trong tam giác vuông, ta có:

\(OM^2= CM.DM \)\(⇔ 2^2 = CM.DM \)\(⇔ 4 = CM.DM  \;\;  (2)\)

Thay \((1)\) và \((2)\) ta có: \(CM.(5 – CM) = 4\)

\(⇔ 5CM – CM^2 – 4 = 0\) 

\(⇔ 4CM – CM^2 + CM – 4 = 0\)

\(⇔ CM(4 – CM) + (CM – 4) = 0\)

\(⇔ CM(4 – CM) – (4 – CM) = 0\)

\(⇔ (CM – 1)(4 – CM) = 0\)

\(⇔ CM – 1 = 0\) hoặc \(4 – CM = 0\)

\(⇔CM = 1\) hoặc \(CM = 4\)

Vì \(CM = CA\) (chứng minh trên) nên \(AC = 1 (cm)\) hoặc \(AC = 4 (cm)\)

Vậy điểm \(C\) cách điểm \(A\) là \(1cm\) hoặc \(4cm\) thì hình thang \(ABDC\) có chu vi bằng \(14.\)

-- Mod Toán 9 HỌC247