Bài tập 54 trang 165 SBT Toán 9 Tập 1

Hướng dẫn giải

Sử dụng kiến thức: 

\(*\)) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì

+)  Điểm đó cách đều hai tiếp điểm.

+) Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.

\(*\)) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

\(*\)) Hệ thức lượng trong tam giác vuông: Bình phương cạnh góc vuông bằng tích cạnh huyền với  hình chiếu cạnh góc vuông đó trên cạnh huyền.

\(*\)) Sử dụng định lí Py-ta-go: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

Lời giải chi tiết

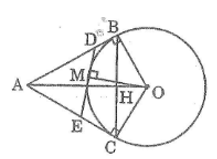
\(a)\) Ta có: \(AB = AC\)  (tính chất hai tiếp tuyến cắt nhau).

Suy ra \(∆ABC\) cân tại A.

\(AO\) là tia phân giác của góc \(BAC\) (tính chất hai tiếp tuyến cắt nhau)

Suy ra \(AO\) là đường cao của tam giác \(ABC\) (tính chất tam giác cân).

Do đó \(AO\) vuông góc với \(BC\) tại \(H\)

Lại có: \(AB ⊥ OB\) (tính chất tiếp tuyến)

Xét tam giác \(ABO\) vuông tại \(B\) có \(BH ⊥ AO\)

Theo hệ thức lượng trong tam giác vuông, ta có:

\(O{B^2} = OH.OA \)\(\Rightarrow OH =\displaystyle  {{O{B^2}} \over {OA}}\)\( =\displaystyle {{{3^2}} \over 5} = 1,8\) (cm)

\(b)\) Áp dụng định lí Pi-ta-go vào tam giác vuông \(ABO,\) ta có:

\(A{O^2} = A{B^2} + B{O^2}\)

Suy ra: \(A{B^2} = A{O^2} - B{O^2} = {5^2} - {3^2} = 16\)

 \(\Rightarrow AB =  4 (cm)\)

Theo tính chất hai tiếp tuyến cắt nhau ta có:

\(DB = DM\)

\(EM = EC\)

Chu vi của tam giác \(ADE\) bằng:

\(AD + DE + EA \)\(= AD + DM + ME + EA\)\(= AD + DB + AE + EC\)

\(= AB + AC = 2AB\) (vì \(AB=AC\) (cmt))

\(= 2.4 = 8 (cm).\)

-- Mod Toán 9 HỌC247