Bài tập 31 trang 116 SGK Toán 9 Tập 1

26 BT SGK

Giải bài 31 tr 116 sách GK Toán 9 Tập 1

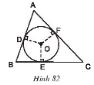
Trên hình 82, tam giác ABC ngoại tiếp đường tròn (O).

a) Chứng minh rằng: 2AD=AB+AC-BC

b) Tìm các hệ thức tương tự hệ thức ở câu a

Bài 31 sẽ nhắc lại cho các bạn tính chất của hai tiếp tuyến cắt nhau, chứng minh hệ thức bằng cách đặt vào các tam giác bằng nhau.

Câu a:

Theo tính chất của hai tiếp tuyến cắt nhau ta có:

\(AD=AF; BD=BE; CF=CE\)

Xét VP:

\(AB+AC-BC=(AD+DB)+(AF+FC)-(BE+EC)\)

\(=(AD+BE)+(AF+CE)-(BE+EC)\)

\(= AD+AF=2AD\)

Câu b:

Các hệ thức tương tự là:

\(2BD=BA+BC-AC\)

\(2CF=CA+CB-AB\)

Nhận xét. Từ bài toán trên ta có các kết quả sau:

AD=AF=p-a; BD=BE=p-b; CE=CF=p-c

trong đó AB=c; BC=a; CA=b và p là nửa chu vi của tam giác ABC.

-- Mod Toán 9 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 31 trang 116 SGK Toán 9 Tập 1 HAY thì click chia sẻ

YOMEDIA

Chứng minh MO//AC?

bởi Hoà Vũ 05/04/2020

Cho nửa đường tròn (O;R)đường kính BC. Kẻ tiếp tuyến Bx với nửa đường tròn. Trên Bx lấy điểm M sao cho BM lớn hơn R. Từ M kẻ tiếp tuyến MA (A là tiếp điểm).

a) Chứng minh MO//AC.

b) Qua O kẻ đường thẳng vuông góc với BC cắt tia CA tại D.Chứng minh tứ giác MOCD là hình bình hành.

c)gọi giao điểm của MD và OA là S ,giao điểm của MA và OD là I ,giao điểm của MO và BD là K. Chứng minh 3 điểm K,I,S thẳng hàng.

Theo dõi (0) 0 Trả lời
Chứng minh ba điểm I; O; A thẳng hàng.

bởi Khánh Ngọc Nguyễn 05/04/2020

Theo dõi (0) 0 Trả lời
Tìm vị trí của M sao cho diện tích tam giác HOA lớn nhất

bởi Khánh Ly 11/02/2020

cho đường tròn (O;R) và điểm A cố định thuộc đường tròn. đường thẳng d tiếp xúc với đương tròn O tại A. Trên đường thẳng d lấy điểm M khác A. kẻ tiếp tuyến MB với đường tròn. Nối OM cắt AB tại H. tìm vị trí của M sao cho a,diện tích tam giác HOA lớn nhất b, Chu vi tam giác HOA lớn nhất

Theo dõi (1) 0 Trả lời