Bài tập 48 trang 164 SBT Toán 9 Tập 1
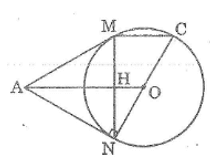
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AM, AN với đường tròn (M, N là các tiếp điểm)
a. Chứng minh rằng OA ⊥ MN
b. Vẽ đường kính NOC. Chứng minh rằng MC // AO
c. Tính độ dài các cạnh của tam giác AMN biết OM = 3cm, OA = 5cm
Hướng dẫn giải chi tiết
a. Ta có: AM = AN (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác AMN cân tại A
Mặt khác AO là đường phân giác của góc MAN (tính chất hai tiếp tuyến cắt nhau)
Suy ra AO là đường cao của tam giác AMN (tính chất tam giác cân)
Vậy OA ⊥ MN.
b. Tam giác MNC nội tiếp trong đường tròn (O) có NC là đường kính nên góc (CMN) = 90o
Suy ra: NM ⊥ MC
Mà OA ⊥ MN (chứng minh trên)
Suy ra: OA // MC
c. Ta có: AN ⊥ NC (tính chất tiếp tuyến)
Áp dụng định lí Pitago vào tam giác vuông AON ta có:
AO2 = AN2 + ON2
Suy ra : AN2 = AO2 – ON2 = 52 – 32 = 16
AN = 4 (cm)
Suy ra: AM = AN = 4 (cm)
Gọi H là giao điểm của AO và MN
Ta có: MH = NH = MN/2 (tính chất tam giác cân)
Tam giác AON vuông tại N có NH ⊥ AO. Theo hệ thức lượng trong tam giác vuông, ta có:
OA.NH = AN.ON ⇒ NH = (AN.ON)/AO = (4.3)/5 = 2,4 (cm)
MN = 2.NH = 2.2,4 = 4,8 (cm)
-- Mod Toán 9 HỌC247
-


Cho (O), đường kính BC. Từ điểm P trên tiếp tuyến của đường tròn tại B, vẽ tiếp tuyến thứ hai PA (A là tiếp điểm) với đường tròn
bởi Trần Mai Anh
 22/11/2019
22/11/2019
Cho (O), đường kính BC. Từ điểm P trên tiếp tuyến của đường tròn tại B, vẽ tiếp tuyến thứ hai PA (A là tiếp điểm) với đường tròn. H là hình chiếu của A lên BC. E là giao điểm của PC và AH
Chứng minh E là trung điểm AH
Theo dõi (0) 1 Trả lời -


Chứng minh M là trung điểm AB biết đường thẳng CD và MB cắt nhau tại A
bởi Hoàng Thị Hương Giang
 15/02/2019
15/02/2019
lấy M là 1 điểm nằm ngoài đường trò (o) .Kẻ tiếp tuyến MB và MC.Kẻ đường kính BOD.Đường thẳng CD và MB cắt nhau tại A. Chứng minh M là trung điểm của AB
Theo dõi (0) 1 Trả lời -


Chứng minh 3 điểm D, A, E thẳng hàng biết tam giác ABC có góc A=90 độ, AH là đường cao
bởi Đào Mai Phương
 03/02/2019
03/02/2019
Cho tam giác ABC có góc A = 90 độ, đường cao AH, vẽ đường tròn (A;AH) kẻ các tiếp tuyến BD, CE với đường tròn (D,E là các tiếp điểm khác H). Chứng minh rằng:
a, 3 điểm D,A,E thẳng hàng
b, DE tiếp xúc với đường tròn đường kính BC
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 31 trang 116 SGK Toán 9 Tập 1
Bài tập 32 trang 116 SGK Toán 9 Tập 1
Bài tập 49 trang 164 SBT Toán 9 Tập 1
Bài tập 50 trang 164 SBT Toán 9 Tập 1
Bài tập 51 trang 164 SBT Toán 9 Tập 1
Bài tập 52 trang 165 SBT Toán 9 Tập 1
Bài tập 53 trang 165 SBT Toán 9 Tập 1
Bài tập 54 trang 165 SBT Toán 9 Tập 1
Bài tập 55 trang 165 SBT Toán 9 Tập 1
Bài tập 56 trang 165 SBT Toán 9 Tập 1
Bài tập 57 trang 165 SBT Toán 9 Tập 1
Bài tập 58 trang 165 SBT Toán 9 Tập 1
Bài tập 59 trang 165 SBT Toán 9 Tập 1
Bài tập 60 trang 166 SBT Toán 9 Tập 1
Bài tập 61 trang 166 SBT Toán 9 Tập 1
Bài tập 62 trang 166 SBT Toán 9 Tập 1
Bài tập 63 trang 166 SBT Toán 9 Tập 1
Bài tập 6.1 trang 166 SBT Toán 9 Tập 1