Bài tập 49 trang 164 SBT Toán 9 Tập 1
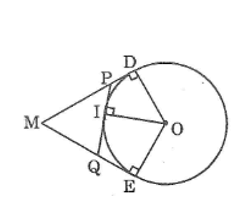
Cho đường tròn (O), điểm M nằm bên ngoài đường tròn. Kẻ tiếp tuyến MD, ME với đường tròn (D, E là các tiếp điểm). Qua I thuộc cung nhỏ DE, kẻ tiếp tuyến với đường tròn, cắt MD và ME theo thứ tự ở P và Q. Biết MD = 4cm, tính chu vi tam giác MPQ
Hướng dẫn giải chi tiết
Ta có: MD = ME (tính chất hai tiếp tuyến cắt nhau)
PD = PI (tính chất hai tiếp tuyến cắt nhau)
QI = QE (tính chất hai tiếp tuyến cắt nhau)
Chu vi tam giác APQ bằng:
MP + PQ + QM
= MP + PI + IQ + QM
= MP + PD + QM + QE
= MD + ME
= 2.MD
= 2.4 = 8 (cm)
-- Mod Toán 9 HỌC247
-


Tính góc ABC, góc BAC biết 2 tiếp tuyến của đường tròn (O) tại B,C cắt nhau ở A
bởi Đại Việt
 04/01/2019
04/01/2019
Cho đường tròn (O;R) và dây cung BC=R. Hai tiếp tuyến của đường tròn (O) tại B,C cắt nhau ở A. Tính góc ABC, góc BAC
Theo dõi (0) 1 Trả lời -


Bài 1: Cho đường tròn ( O;R) và một điểm A nằm ngoài đường tròn (O) sao cho OA= 2R. Từ A vẽ tiếp tuyến của đường tròn (O), B là tiếp điểm
1) Chứng minh tam giác ABO vuông tai B và tính độ dài AB theo R
2) Từ B vẽ dây cung BC của (O) vuông góc với cạnh OA tại H. Chứng minh AC là tiếp tuyến của (O)
3) Chứng minh tam giác ABC đều
4) Vẽ (K) đường kính AC, chứng minh BK vuông góc với AC
5) Từ H vẽ đường thẳng vuông góc với AB tại D. Đường tròn đường kính AC cắt cạnh DC tại E. Gọi F là trung điểm của cạnh OB. Chứng minh 3 điểm A, E, F thẳng hàng
Mình sắp thi rồi ai giúp mình với ạ. Mình cảm ơn nhiều lắm
Theo dõi (0) 1 Trả lời -


Chứng minh HB=HC biết đường tròn (O) có bán kính 15cm, dây BC có độ dài 24cm
bởi Trần Tuấn Anh
 10/12/2018
10/12/2018
Cho đường tròn (Ô) bán kính 15 cm dây BC có độ dài 24 cm. Các tiếp tuyến của đường tròn tại B và C cắt nhau ở A. Gọi H là giao của OA và BC
a) CM: HB=HC
b) Tính OH, OA
Theo dõi (0) 3 Trả lời
Bài tập SGK khác
Bài tập 32 trang 116 SGK Toán 9 Tập 1
Bài tập 48 trang 164 SBT Toán 9 Tập 1
Bài tập 50 trang 164 SBT Toán 9 Tập 1
Bài tập 51 trang 164 SBT Toán 9 Tập 1
Bài tập 52 trang 165 SBT Toán 9 Tập 1
Bài tập 53 trang 165 SBT Toán 9 Tập 1
Bài tập 54 trang 165 SBT Toán 9 Tập 1
Bài tập 55 trang 165 SBT Toán 9 Tập 1
Bài tập 56 trang 165 SBT Toán 9 Tập 1
Bài tập 57 trang 165 SBT Toán 9 Tập 1
Bài tập 58 trang 165 SBT Toán 9 Tập 1
Bài tập 59 trang 165 SBT Toán 9 Tập 1
Bài tập 60 trang 166 SBT Toán 9 Tập 1
Bài tập 61 trang 166 SBT Toán 9 Tập 1
Bài tập 62 trang 166 SBT Toán 9 Tập 1
Bài tập 63 trang 166 SBT Toán 9 Tập 1
Bài tập 6.1 trang 166 SBT Toán 9 Tập 1