Giải bài 32 tr 42 sách BT Toán lớp 7 Tập 2
Chứng minh rằng nếu một tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng tính chất: Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.
Sử dụng tính chất hai tam giác bằng nhau.
Lời giải chi tiết
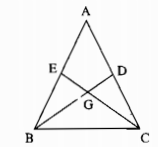
Giả sử \(∆ABC\) có hai đường trung tuyến \(BD, CE \) và \(BD = CE.\) Gọi \(G\) là giao điểm \(BD\) và \(CE.\)
Khi đó, G là trọng tâm của tam giác ABC. Suy ra:
\(\displaystyle BG = {2 \over 3}B{\rm{D}}\) (tính chất đường trung tuyến)
\(\displaystyle CG = {2 \over 3}CE\) (tính chất đường trung tuyến)
Mà \(BD = CE\)
Suy ra: \(BG = CG\)
\( \Rightarrow BG + GD = CG + GE\)
\( \Rightarrow GD = GE\)
Xét \(∆BGE\) và \(∆CGD:\)
+) \(BG = CG\) (chứng minh trên)
+) \(\widehat {BGE} = \widehat {CG{\rm{D}}}\) (đối đỉnh)
+) \(GE = GD\) (chứng minh trên)
Do đó: \(∆BGE = ∆CGD\) (c.g.c)
\( \Rightarrow BE = CD\) (1)
\(\displaystyle BE = {1 \over 2}AB\) (vì \(E\) là trung điểm \(AB)\) (2)
\(\displaystyle C{\rm{D = }}{1 \over 2}AC\) (vì \(D\) là trung điểm \(AC) \) (3)
Từ (1), (2) và (3) suy ra: \(AB = AC.\)
Vậy \(∆ABC\) cân tại \(A.\)
-- Mod Toán 7 HỌC247
-


Chứng minh BN=CM và tam giác IBC cân biết tam giác ABC cân tại A có 2 đường trung tuyến
bởi Nguyễn Thị Thanh
 10/04/2019
10/04/2019
cho tam giác ABC cân tại A , hai đường trung tuyến BN và CM cắt nhau tại I . cmr:
a. BN=CM và tam giác IBC cân
b. điểm I cách đều hai cạnh AB và AC
c. AI là trung trực của BC
d. từ B kẻ Bx vuông góc với AB . từ C kẻ Cy vuông góc với AC . Bx cắt Cy tại K . cmr 3 điểm A , I , K thẳng hàng
e. giả sử góc BAC = 60 độ , CA = CB = 8 cm . tính AI
Theo dõi (0) 1 Trả lời -


Chứng minh I, G, C thẳng hàng biết tam giác ABC có AB=9cm, AC=12cm, BC=15cm
bởi thi trang
 10/04/2019
10/04/2019
Cho tam giác ABC có AB=9cm , AC=12cm , BC=15cm . AM là đường trung tuyến của tam giác ABC . Kẻ MH vuông góc với AC . Trên tia đối của MH lấy K sao cho MH=MK
a, CM tam giác ABC là tam giác vuông
b , CM tam giác MHC= tam giác MKB
c, Gọi G là giao điểm của BH và AM. I là trung điểm của AB. CM I , G , C thẳng hàng
Theo dõi (0) 1 Trả lời -


Nêu các tính chất về đường trung tuyến của tam giác?
bởi Lê Gia Bảo
 10/04/2019
10/04/2019
- Nêu cách xác định trung điểm của đoạn thẳng?
- Nêu các tính chất về đường trung tuyến của tam giác?
- Nêu tính chất về trọng tâm của tam giác?
Theo dõi (0) 1 Trả lời -


Chứng minh 3 đường thẳng AC, BD, KE cùng đi qua 1 điểm biết tam giác ABC vuông tại A
bởi Nguyễn Tiểu Ly
 10/04/2019
10/04/2019
Cho tam giác ABC vuông tại C; góc A bằng 600, tia phân giác của góc BAC cắt BC tại E, kẻ EK vuông góc với AB (K thuộc AB), kẻ BD vuông góc với tia AE (D thuộc tia AE). Chứng minh:
a) AC = AK.
b) KA = KB.
c) Ba đường thẳng AC, BD, KE cùng đi qua một điểm.
Theo dõi (0) 1 Trả lời -


Chứng minh BI=IK=KD biết tam giác ABC có các đường trung tuyến BE, CF cắt nhau tại I
bởi Hương Lan
 10/04/2019
10/04/2019
Cho tam giác ABC có các đường trung tuyến BE; CF cắt nhau tại I .
a, C/minh: \(BE+CF>\dfrac{3}{2}BC\)
b, Trên tia đối tia EB lấy điểm D sao cho ED = EB. Gọi M là trung điểm của AD , CM cắt BD tại K . C/minh: BI = IK = KD
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC trung tuyến AM trọng tâm G.Chứng minh:
SAMB = SAMC
Theo dõi (0) 1 Trả lời -


Cho △ABC có BC = 2.AB, M là trung điểm BC, D là trung điểm BM. CMR AC = 2.AD
Theo dõi (0) 1 Trả lời -


Tính độ dài trung tuyến BN biết tam giác ABC vuông tại A có AC=5cm, trung tuyến AM=3,5
bởi bala bala
 11/04/2019
11/04/2019
Cho tam giác ABC vuông tại A. biết ÁC= 5cm, trung tuyến AM= 3.5 cm
a) AB=? , BC=?
b) tính các đường trung tuyến BN
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A có AB=3cm; AC= 6cm. Gọi E là trung điểm của AC, tia phân giác góc A cắt BC tại D.
a, Tính độ dài BC
b, C/m: tam giác BAD= tam giác EAD
c, Đường thẳng ED cắt AB tại M. Chứng minh tam giác BAC = tam giác EAM. Từ đó suy ra tam giác MAC vuông cân.
d, C/minh: DC= 2BD
Các bạn giúp mình phần d thôi nhé. Cảm ơn ạ
Theo dõi (0) 1 Trả lời -


Chứng minh góc GCB < góc GBC biết các đường trung tuyến BD và CE cắt nhau tại G
bởi Nguyễn Trà Long
 11/04/2019
11/04/2019
Cho tam giác ABC . Các đường trung tuyến BD và CE cắt nhau tại G ; biết rằng BC < CE .Chứng minh:
a)G là trọng tâm của tam giác ABC
b) góc GCB < góc GBC
Theo dõi (0) 1 Trả lời -


Tính AM, BN, CE biết tạm giác ABC vuông tại A có 3 đường trung tuyến AM, BN, CE cắt nhau tại O
bởi Lê Nhật Minh
 11/04/2019
11/04/2019
Cho tam giac ABC vuong tai A . Ba duong trung tuyen AD BE CF. Ba duong trung tuyen AM , BN , CE cat nhau tai O
a tinh AM , BN , CE
b Tinh dt tam giac BOC
Theo dõi (0) 1 Trả lời -


Chứng minh AH vuông góc MI biết tam giác ABC cân tại A có I là trung điểm của HD
bởi Thanh Nguyên
 11/04/2019
11/04/2019
Cho \(\Delta ABC\) cân tại A ( góc A < 90 độ ), có ba đường cao AH, BD, CE. Chứng minh :
a, \(\Delta ABD\) = \(\Delta ACE\)
b, \(\Delta HDC\) cân tại H
c, Kẻ HM vuông góc với AC (\(M\in AC\)). Chứng minh : DM = MC
d, Gọi I là trung điểm của HD. Chứng minh : AH vuông góc với MITheo dõi (0) 1 Trả lời -


Chứng minh MI=IK=KN biết tam giác ABC có các đường trung tuyến của BD và CE cắt nhau ở G
bởi Duy Quang
 11/04/2019
11/04/2019
1) Cho tam giác ABC, các đường trung tuyến của BD và CE cắt nhau ở G. Gọi I, K theo thứ tự là trung điểm của GB, GC . CMR: DE// IK ; DE=IK
2)Cho tam giác ABC, các đường trung tuyến của BD, CE. Gọi M, N theo thứ tự là trung điểm của BE , CD . Gọi I, K theo thứ tự là giao điểm của MN với BD, CE. CMR: MI=IK=KN
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A có đường cao AH.
a, Chứng minh tam giác ABH = tam giác ACH và AH là tia phân giác của góc BAC.
b, Cho BH= 8cm, AB= 10cm.Tính AH.
c,, Gọi E là trung điểm của AC và G là giao điểm của BE và AH.Tính HG.
d, Vẽ Hx song song với AC, Hx cắt AB tại F. Chứng minh C, G, F thẳng hàng.Theo dõi (0) 1 Trả lời -


Tính khoảng cách từ đỉnh A đến trọng tâm G của tam giác ABC vuông tại A
bởi Trần Thị Trang
 12/04/2019
12/04/2019
Cho tam giác ABC vuông tại A có AB = 9cm; AC = 12cm. Tính khoảng cách từ đỉnh A đến trọng tâm G của tam giác.
Theo dõi (0) 1 Trả lời -


chứng minh rằng trong một tam giác,nếu trung tuyến ứng với một cạnh bằng một nửa cạnh ấy thì tam giác đó là tam giác vuông
Theo dõi (0) 1 Trả lời -


Tính CG biết tam giác ABC cân tại A có BN, CM là trung tuyến, G là trọng tâm
bởi Trần Hoàng Mai
 12/04/2019
12/04/2019
Vẽ \(\Delta\)ABC cân tại A; BN và CM là các trung tuyến, G là trọng tâm của tam giác.Tính CG, biết CM=9
Theo dõi (0) 1 Trả lời





