Giải bài 31 tr 42 sách BT Toán lớp 7 Tập 2
Cho hình 7. Điền vào chỗ trống:
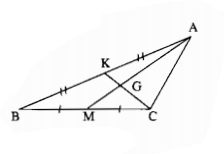
\(GK = ….CK; AG = … GM;\) \(GK = … CG;\)
\(AM = ….AG; AM = … GM.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng tính chất:
Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.
Lời giải chi tiết
Từ hình vẽ ta thấy, \(AM, CK\) là hai đường trung tuyến của tam giác \(ABC\) và hai đường này cắt nhau tại \(G\) nên \(G\) là trọng tâm tam giác \(ABC\).
Suy ra: \(CG=\dfrac{2}{3}CK;AG=\dfrac{2}{3}AM\)
Do đó: \(\displaystyle GK = {1 \over 3}CK;AG = 2GM\)
\(\displaystyle GK = {1 \over 2}CG;AM = {3 \over 2}AG\)
\(AM = 3GM\)
-- Mod Toán 7 HỌC247
-


Chứng minh a^2+b^2=5c^2 biết tam giác ABC có 2 đường trung tuyến AM và BN
bởi Nguyễn Anh Hưng
 25/02/2019
25/02/2019
Cho \(\Delta ABC\), 2 đường trung tuyến \(AM;BN\) vuông góc với nhau tại G biết \(AB=a;BC=b;CA=c\). CMR \(a^2+b^2=5c^2\)
Theo dõi (0) 1 Trả lời -


Chứng minh trong tam giác vuông có 1 cạnh bằng một nửa cạnh huyền
bởi Nguyễn Lê Thảo Trang
 25/02/2019
25/02/2019
Chứng minh định lí sau : trong tam giác vuông có một cạnh bằng một nửa cạnh huyền thì góc đối diện với đó bằng 30 độ
Theo dõi (0) 1 Trả lời -


Chứng minh các cạnh của tam giác BGD bằng 2/3 các cạnh trung tuyến của tam giác ABC
bởi Hoai Hoai
 25/02/2019
25/02/2019
Cho \(\Delta ABC\) có các trung tuyến \(AM;BN;CP\) cắt nhau tại trọng tâm G. Trên tia AM lấy D sao cho G là trung điểm của AD.
a/ C.m các cạnh của \(\Delta BGD=\dfrac{2}{3}\) các trung tuyến của \(\Delta ABC\)
b/ C.m các trung tuyến của \(\Delta BGD=\dfrac{1}{2}\) các cạnh của \(\Delta ABC\)
c/ Nêu cách dựng \(\Delta ABC\) khi biết độ dài 3 đường trung tuyến \(AM;BN;CP\)
Theo dõi (0) 1 Trả lời -


Chứng minh M, I, K thẳng hàng biết tam giác ABC vuông tại A có M là trung điểm AC
bởi Nhat nheo
 08/04/2019
08/04/2019
Cho tam giác ABC vuông tại A, gọi M là trung điểm của AC. Trên tia đối của tia MB lấy điểm D sao cho MD=MB. Đường thẳng qua B song song với AC cắt tia DC tại N.
a) Chứng minh \(\Delta AMB=\Delta CDM\)
b) Chứng minh AD// BC
c) Chứng minh MC là tia phân giác của \(\stackrel\frown{DMN}\)
d) Gọi I là trung điểm của BN ; K là giao điểm của BC và AN. Chứng minh M, I, K thẳng hàng
Theo dõi (0) 1 Trả lời -


Đường trung tuyến là gì?
bởi Nguyễn Phương Khanh
 26/09/2018
26/09/2018
Đường trung tuyến như thế nào ?
Theo dõi (0) 1 Trả lời -


Chứng minh BG đi qua trung điểm E của AC biết E là trung điểm AB, AH cắt CE tại G
bởi Bánh Mì
 08/04/2019
08/04/2019
Cho tam giác ABC cân tại A ( Â < 90 độ ) vẽ đường cao AH .
a) CM : tam giác ABH = tam giác ACH
b) Trên tia đối của tia HA lấy điểm D sao cho HA = HD . CM : AC = DC
c) Gọi E là trung điểm của AB , AH cắt CE tại G . CM đường thẳng BG đi qua trung điểm F của AC
d) Đường thẳng BF cắt đường thẳng DC tại K . CM tam giác AKD vuông .
Theo dõi (0) 1 Trả lời -


Cho 3 điểm a b c không thẳng hàng.
Hãy tìm điểm D cách đều 3 điểm A, B, C
Theo dõi (0) 1 Trả lời -


ho tam giac ABC,lay diem D thuoc tia doi cua tia BC sao cho BD=BA,lay diem E thuoc tia doi cua tia CB sao cho CE=CA.2diem H va K lan luot la trung diem cua AD va AE. I la giao diem cua HB va KC.
cm: a.AH la duong gi doi voi tam giac ABD
b.AI la tia phan giac cua goc ABC
c.duong trung truc cua DE di qua diem I
Theo dõi (0) 1 Trả lời -


Chứng minh BF=CE và BF//CE biết tam giác ABC có BM, CN cắt nhau tại G
bởi Lê Nguyễn Hạ Anh
 08/04/2019
08/04/2019
cho tam giác ABC . hai trung tuyến BM ,CN cắt tại G. Tia đối tia MG lấy E sao cho ME=MG . tia đối tia NG lấy F sao cho NF=NG . Chứng minh BF=CE, BF//CE
Theo dõi (0) 1 Trả lời -


Chứng minh 3 tam giác ABC, DEF, MPN có cùng trọng tâm biết tam giác ABC đều
bởi Anh Nguyễn
 08/04/2019
08/04/2019
Chotam giác ABC đều. Trên AB lấy điểm D sao cho BD=1/3BA. Qua D kẻ đường vuông góc với AB cắt BC tại E. Qua E kẻ đường vuông góc với BC cắt AC tại F.
a) CMR: DF vuông góc với AC
b) CMR: tam giác DEF đều
c) Trên tia đối của các tia DE; FD; EF lần lượt lấy các điểm P; M; N sao cho DP=FM=EN.
Tam giác MNP là tam giác gì? C/m
d) CMR: Ba tam giác ABC; DEF; MPN có chung trọng tâm.
Theo dõi (0) 1 Trả lời -


Tính tỉ số GM/AG biết tam giác ABC có AM là trung tuyến, G là trọng tâm, AM=9cm
bởi Thùy Nguyễn
 09/04/2019
09/04/2019
cho tam giác ABC AM là trung tuyến , G là trọng tâm , AM = 9cm
Tính tỉ số GM/AG?Theo dõi (0) 1 Trả lời -


Chứng minh tam giác HCB cân biết tam giác ABC cân tại A có trung tuyến BP và CQ
bởi Hoàng My
 09/04/2019
09/04/2019
cho \(\Delta ABC\) cân tại A trung tuyến BP và CQ cắt nhau tại H
a/ chứng minh \(\Delta ABP\) = \(\Delta ACQ\)
b/ chứng minh \(\Delta HCB\) cân
Theo dõi (0) 1 Trả lời -


Chứng minh AF=2FI biết tam giác ABC nhọn có I là trung điểm BE, AI cắt BG tại F
bởi Mai Đào
 09/04/2019
09/04/2019
Cho tam giác nhọn ABC.Trung tuyến AM và CN cắt nhau tại G.Trên tia đối của tia MA lấy điểm E sao cho ME = MG
a) Chứng minh BG = CE
b) Gọi I là trung điểm của BE,đoạn thẳng AI cắt BG tại F.Chứng minh AF = 2FI
Theo dõi (0) 1 Trả lời -


Các tìm kiếm liên quan đến cho tam giác ABC, trung tuyến AD, BE, CF cắt nhau tại G. chứng minh \(AD< \dfrac{AB+AC}{2}\)
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại B, cạnh BC = 18,6 cm; hai trung tuyến BM, CN vuông góc với nhau. Tính CN
Theo dõi (0) 1 Trả lời -


So sánh các cạnh của tam giác ICF với các trung tuyến AD, BE, CF của tam giác ABC
bởi hi hi
 10/04/2019
10/04/2019
Cho tam giác ABC, ba đường trung tuyến AD, BE,CF. Từ F kẻ đường thẳng song song với AD cắt tia ED tại I. So sánh các cạnh của tam giác ICF với các trung tuyến của tam giác ABC.
Theo dõi (0) 1 Trả lời -


Tính AM biết tam giác ABC có AM là đường trung tuyến, G là trọng tam giác và AG=5cm
bởi Nguyễn Xuân Ngạn
 10/04/2019
10/04/2019
Cho tam giác ABC , AM là đường trung tuyến. gọi G là trọng tâm của tam giác, biết AG= 5cm. Tính AM
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 29 trang 67 SGK Toán 7 Tập 2
Bài tập 30 trang 67 SGK Toán 7 Tập 2
Bài tập 32 trang 42 SBT Toán 7 Tập 2
Bài tập 33 trang 42 SBT Toán 7 Tập 2
Bài tập 34 trang 42 SBT Toán 7 Tập 2
Bài tập 35 trang 42 SBT Toán 7 Tập 2
Bài tập 36 trang 43 SBT Toán 7 Tập 2
Bài tập 37 trang 43 SBT Toán 7 Tập 2





