Giải bài tập SGK Bài 4 Chương 3 Hình học 7 Tập 2

Cho G là trọng tâm của tam giác DEF với đường trung tuyến DH (h. 24)

Trong các khẳng định sau đây, khẳng định nào đúng?

\(\begin{array}{l} \frac{{DG}}{{DH}} = \frac{1}{2};\frac{{DG}}{{GH}} = 3\\ \frac{{GH}}{{DH}} = \frac{1}{3};\frac{{GH}}{{DG}} = \frac{2}{3} \end{array}\)

Cho hình 25. Hãy điền số thích hợp vào chỗ trống trong các đẳng thức sau:

a) MG=...MR; GR=...MR; GR=...MG

b) NS=...NG; NS=...GS; NG=...GS

Biết rằng: Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền. Hãy giải bài toán sau:

Cho tam giác vuông ABC có hai cạnh góc vuông AB=3cm, AC=4cm. Tính khoảng cách từ đỉnh A tới trọng tâm G của tam giác ABC.

Chứng minh định lí: Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau

Hãy chứng minh định lí đảo của định lí trên: nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân

Cho tam giác DEF cân tại D với đường trung tuyến DI.

a) Chứng minh tam giác DEI=tam giác DFI

b) Cho biết số đo của hai góc DIE và DIF

c) Biết DE=DF=13cm, EF=10cm, hãy tính độ dài đường trung tuyến DI

Gọi G là trọng tâm của tam giác đều ABC. Chứng minh rằng:

GA=GB=GC

Hướng dẫn: Áp dụng định lí ở bài tập 26

Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'

a) So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC

b) So sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC

Cho hình 7. Điền vào chỗ trống:

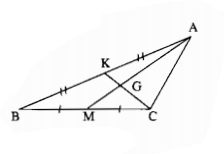
\(GK = ….CK; AG = … GM;\) \(GK = … CG;\)

\(AM = ….AG; AM = … GM.\) 

Chứng minh rằng nếu một tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân.

Tam giác \(ABC\) cân tại \(A\) có \(AB = AC = 34cm, BC = 32cm.\) Kẻ đường trung tuyến \(AM.\)

a) Chứng minh rằng \(AM \bot BC\)

b) Tính độ dài \(AM.\) 

Gọi \(\displaystyle G\) là trọng tâm của tam giác \(\displaystyle ABC.\) Vẽ điểm \(\displaystyle D\) sao cho \(\displaystyle G\) là trung điểm của \(\displaystyle AD.\) Chứng minh rằng:

a) Các cạnh của tam giác \(\displaystyle BGD\) bằng \(\displaystyle \displaystyle {2 \over 3}\) các đường trung tuyến của tam giác \(\displaystyle ABC\) 

b) Các đường trung tuyến của tam giác \(\displaystyle BGD\) bằng một nửa các cạnh của tam giác \(\displaystyle ABC.\)

Tam giác \(\displaystyle ABC\) có \(\displaystyle BC = 10cm,\) các đường trung tuyến \(\displaystyle BD\) và \(\displaystyle CE.\) Chứng minh rằng \(\displaystyle BD + CE > 15cm.\) 

Cho tam giác \(\displaystyle ABC.\) Trên tia đối của tia \(\displaystyle BA\) lấy điểm \(\displaystyle D\) sao cho \(\displaystyle BD = BA.\) Trên cạnh \(\displaystyle BC\) lấy điểm \(\displaystyle E\) sao cho \(\displaystyle BE = {1 \over 3}BC\). Gọi \(\displaystyle K\) là giao điểm của \(\displaystyle AE\) và \(\displaystyle CD. \) Chứng minh rằng \(\displaystyle DK = KC.\) 

Theo kết quả của bài 64 chương II, SBT Toán 7 tập 1 ta có: Đoạn thẳng nối trung điểm hai cạnh của một tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

Vận dụng kết quả trên để giải bài toán sau: Cho tam giác  \(\displaystyle ABC,\)  đường trung tuyến \(\displaystyle AD.\)  Kẻ đường trung tuyến \(\displaystyle BE\) cắt \(\displaystyle AD\) ở \(\displaystyle G.\) Gọi \(\displaystyle I, K\) theo thứ tự là trung điểm của \(\displaystyle GA, GB.\) Chứng minh rằng:

a) \(\displaystyle IK // DE, IK = DE\) 

b) \(\displaystyle {\rm{A}}G = {2 \over 3}A{\rm{D}}\)

Cho tam giác \(ABC\) vuông tại \(A,\) đường trung tuyến \(AM.\) Trên tia đối của tia \(MA\) lấy điểm \(D\) sao cho \(MD = MA.\)

a) Tính số đo góc \(ABD.\)

b) Chứng minh: \(∆ABC = ∆BAD.\)

c) So sánh độ dài \(AM\) và \(BC.\)

Tam giác \(\displaystyle ABC\) có đường trung tuyến \(\displaystyle AM\) bằng nửa cạnh \(\displaystyle BC.\) Chứng minh rằng \(\displaystyle \widehat {BAC} = 90^\circ \).