Giải bài tập Toán 12 Chương 3 Bài 3 Ứng dụng của tích phân trong hình học

Tính diện tích hình phẳng giới hạn bởi các đường:

a) $y = x^2, y = x + 2$;   

b) $y = |lnx|, y = 1$;

c) $y = (x - 6)^2, y = 6x- x^2$

Tính diện tích hình phẳng giới hạn bởi đường cong y = x² +1, tiếp tuyến với đường thẳng này tại điểm M(2;5) và trục Oy.

Parabol $y=\frac{x^{2}}{2}$ chia hình tròn có tâm tại gốc tọa độ, bán kính $2 \sqrt {2}$ thành hai phần. Tìm tỉ số diện tích của chúng.

Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh trục Ox:

a) $\small y = 1 - x^2 , y = 0$ ;

b) $\small y = cosx, y = 0, x = 0, x = \pi$ ;

c)  $\small y = tanx, y = 0, x = 0,x=\frac{\pi }{4}$ ;

Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt  $\widehat{POA}=\alpha$ và $OM=R, \left ( 0\leq \alpha \leq \frac{\pi }{3}, R>0 \right )$.

Gọi V là khối tròn xoay thu được khi quay tam giác đó xung quanh Ox (H.63).

a) Tính thể tích của V theo α và R.      

b) Tìm $\small \alpha$ sao cho thể tích V là lớn nhất.  

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = sinx + 1, trục hoành và hai đường thẳng x = 0 và $x = \frac{{7\pi }}{6}$ 

Tính diện tích hình phẳng giới hạn bởi:

a) Đồ thị hàm số y = cos²x trục hoành, trục tung và đường thẳng x = π
b) Đồ thị hai hàm số $y = \sqrt x$ và $y = \sqrt[3]{x}$
c) Đồ thị hàm số y = 2x² và y = x⁴ −2x² trong miền x ≥ 0 .

Tính diện tích hình phẳng giới hạn bởi:

a) Đồ thị các hàm số y = x² − 4, y = −x² − 2x và đường thẳng x = −3, x = −2
b) Đồ thị hai hàm số y = x² và y = −x² − 2x
c) Đồ thị hàm số y = x³ − 4x, trục hoành, đường thẳng x = - 2 và đường thẳng x = 4

Tính thể tích của vật thể nằm giữa hai mặt phẳng x = −1 và x = 1, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (−1 ≤ x ≤ 1) là một hình vuông cạnh là $2\sqrt {1 - {x^2}}$ 

Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = π, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x(0 ≤ x ≤ π) là một tam giác đều cạnh $2\sqrt {{\rm{sinx}}}$

Cho hình phẳng A giới hạn bởi các đường y = 0$, \mathrm{x }= 4$, và $y = \sqrt x  - 1$. Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành

Cho hình phẳng B giới hạn bởi các đường x = 2/y, y = 1 và y = 4. Tính thể tích của khối tròn xoay tạo thành khi quay hình B quanh trục tung

Cho hình phẳng B giới hạn bởi các đường $x = \sqrt 5 {y^2},x = 0,y =  - 1$ và y = 1. Tính thể tích của khối tròn xoay tạo thành khi quay hình B quanh trục tung.

Tính diện tích hình phẳng giới hạn bởi:

a) Đồ thị các hàm số y = x, y = 1 và $y = \frac{{{x^2}}}{4}$ trong miền x ≥ 0, y ≤ 1.

b) Đồ thị hai hàm số y = x⁴ − 4x² + 4, y = x², trục tung và đường thẳng x = 1

c) Đồ thị các hàm số y = x², y = 4x − 4 và y = −4x – 4

Tính diện tích hình phẳng giới hạn bởi:

a) Đồ thị hai hàm số y = x² + 1 và y = 3 – x

b) Các đường có phương trình x = y³, y = 1, và x = 8

c) Đồ thị của hàm số $y = \sqrt x$,y = 6 − x và trục hoành.

Tính thể tích của vật thể T nằm giữa hai mặt phẳng x = 0 và x = π, biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0 ≤ x ≤ π) là một hình vuông cạnh là $2\sqrt {\sin x}$

Cho hình phẳng A giới hạn bởi các đường y = x², x = 0 và x = 2. Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành.

Cho hình phẳng A giới hạn bởi các đường y = cosx,y = 0, x = 0 và x = π/4. Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành.

Cho hình phẳng A giới hạn bởi các đường $y = x{e^{\frac{x}{2}}}$ y = 0, x = 0 và x = 1. Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành.

Cho hình phẳng B giới hạn bởi các đường $x = \sqrt {2\sin 2y} ,x = 0,y = 0$, x = 0,y = 0, $y = \frac{\pi }{2}$. Tính thể tích của khối tròn xoay tạo thành khi quay hình B quanh trục tung.

Tính diện tích hình phẳng giới hạn bởi các đường sau:

a) $y = 2x - {x^2},x + y = 2$;

b) $y = {x^3} - 12x,y = {x^2}$;

c) $x + y = 1,x + y =  - 1,x - y = 1,x - y =  - 1$;

d) $y = \frac{1}{{1 + {x^2}}},y = \frac{1}{2}$;

e) $y = {x^3} - 1$ và tiếp tuyến với $y = {x^3} - 1$ tại điểm (-1;-2).

Tính thể tích vật thể:

a) Có đáy là một tam giác cho bởi: y = x , y = 0 , và x = 1. Mỗi thiết diện vuông góc với trục Ox là một hình vuông.

b) Có đáy là một hình tròn giới hạn bởi x² + y² = 1. Mỗi thiết diện vuông góc với trục Ox là một hình vuông.

Tính thể tích các khối tròn xoay khi quay hình phẳng xác định bởi:

a) y = 2 – x², y = 1, quanh trục Ox.

b) y = 2x – x², y = x, quanh trục Ox.

c) $y = {(2x + 1)^{\frac{1}{3}}},x = 0,y = 3$ quanh trục Oy.

Tính thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các đường $y = \frac{1}{x}$, y = 0, x = 1 và x = a (a > 1). Gọi thể tích đó là V(a). Xác định thể tích của vật thể khi $a \to  + \infty$ (tức là $\mathop {\lim }\limits_{a \to  + \infty } V(a)$).

Một hình phẳng được giới hạn bởi $y = {e^{ - x}},y = 0,x = 0,x = 1$. Ta chia đoạn [0;1] thành n phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật con như dưới).

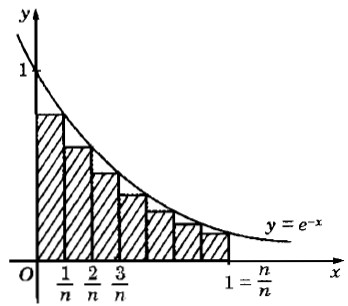
a) Tính diện tích S_n của hình bậc thang (tổng diện tích của n hình chữ nhật con).

b) Tìm $\mathop {\lim }\limits_{n \to \infty } {S_n}$ và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân.

Cho hình phẳng R giới hạn bởi các đường sau đây: ${y_1} = {f_1}\left( x \right).{y_2} = {f_2}\left( x \right)$ (${f_1},{f_2}$ là các hàm số liên tục trên đoạn [a;b]), x = a và x = b. Hãy chỉ ra công thức sai trong việc tính diện tích hình R.

A. $\int \limits_a^b \left| {{f_1}\left( x \right) - {f_2}\left( x \right)} \right|dx$

B. $\int \limits_a^b \left| {{f_2}\left( x \right) - {f_1}\left( x \right)} \right|dx$

C. $\left| {\int \limits_a^b \left| {{f_1}\left( x \right) - {f_2}\left( x \right)} \right|dx} \right|$

D. $\left| {\int \limits_a^b \left[ {{f_1}\left( x \right) - {f_2}\left( x \right)} \right]dx} \right|$

Diện tích hình phẳng P giới hạn bởi các đường ${y_1} = x,{y_2} = 2x,{y_3} = 2 - x$ bằng:

A. 1                      

B. $\frac{2}{3}$

C. 2                     

D. $\frac{2}{3}$

Diện tích của hình phẳng giới hạn bởi các đường ${y_1} = {x^3};{y_2} = 4x$ bằng

A. 0                   

B. 4

C. 8                   

D. −8

Cho hình phẳng H giới hạn bởi các đường y = f(x), y = 0, x = b và x = a (trong đó hàm số f(x) liên tục trên đoạn [b;a]). Thể tích khối tròn xoay tạo nên bởi phép quay hình H quanh trục Ox được cho bởi công thức:

A. $\pi \int \limits_a^b {f^2}\left( x \right)dx$   

B. $\int \limits_a^b {f^2}\left( x \right)dx$

C. $\pi \int \limits_b^a {f^2}\left( x \right)dx$

D. $\int \limits_a^b {\left[ {\pi f\left( x \right)} \right]^2}dx$

Quay hình phẳng Q giới hạn bởi các đường ${y_1} = \sin x,{y_2} = \frac{{2x}}{\pi }$ quanh trục Ox, ta được một khối tròn xoay. Khi đó thể tích của khối tròn xoay này bằng

A. $\frac{1}{6}$                    

B. $\frac{\pi }{6}$

C. 8                      

D. $\frac{{{\pi ^2}}}{6}$

Quay hình phẳng G giới hạn bởi các đường y = x³, y = 1, x = 0 xung quanh trục Oy. Khi đó thể tích của khối tròn xoay này bằng:

A. $\pi$                   

B. $\frac{5}{3}\pi$

C. $\frac{3}{5}\pi$               

D. $\frac{3}{5}$