Bài tập 3.35 trang 178 SBT Toán 12
Một hình phẳng được giới hạn bởi \(y = {e^{ - x}},y = 0,x = 0,x = 1\). Ta chia đoạn [0;1] thành n phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật con như dưới).
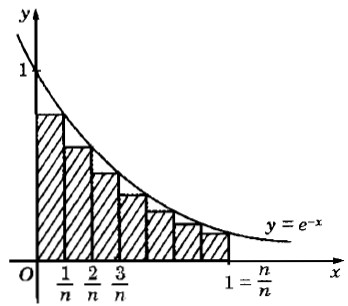
a) Tính diện tích Sn của hình bậc thang (tổng diện tích của n hình chữ nhật con).
b) Tìm \(\mathop {\lim }\limits_{n \to \infty } {S_n}\) và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân.
Hướng dẫn giải chi tiết
a) Ta có:
\(\begin{array}{l}
{S_1} = \frac{1}{n}.{e^{ - \frac{1}{n}}}\\
{S_2} = \frac{1}{n}.{e^{ - \frac{2}{n}}}\\
,...,{S_n} = \frac{1}{n}.{e^{ - \frac{n}{n}}}
\end{array}\)
\(\begin{array}{l}
\Rightarrow {S_n} = \frac{1}{n}\left( {{e^{ - \frac{1}{n}}} + {e^{ - \frac{2}{n}}} + ... + {e^{ - \frac{n}{n}}}} \right)\\
= \frac{1}{n}.{e^{ - \frac{1}{n}}}\frac{{1 - {{\left( {{e^{ - \frac{1}{n}}}} \right)}^n}}}{{1 - {e^{ - \frac{1}{n}}}}} = \frac{1}{n}.\frac{{1 - {e^{ - 1}}}}{{{e^{\frac{1}{n}}} - 1}}
\end{array}\)
b) \(\mathop {\lim }\limits_{n \to \infty } {S_n} = 1 - {e^{ - 1}}\)
Mặt khác: \(S = 1\int\limits_0^1 {{e^{ - x}}} dx = \left. { - {e^{ - x}}} \right|_0^1 = 1 - {e^{ - 1}}\)
Do đó \(\mathop {\lim }\limits_{n \to \infty } {S_n} = 1 - {e^{ - 1}} = \int \limits_0^1 {e^{ - x}}dx = S\)
-- Mod Toán 12 HỌC247
-


Tính a+b biết diện tích giới hạn bởi y=x^2-4x+5 và tiếp tuyến tại A(1;2), B(4;5) = a/b
bởi Mai Anh
 26/09/2018
26/09/2018
diện tích hình phẳng giới hạn bởi đồ thị y=x^2-4x+5 và tiếp tuyến với đồ thị hàm số tại A(1;2) B(4;5) có kết quả dạng a/b khi đó a+b bằng
Theo dõi (0) 1 Trả lời -


Tính diện tích hình phẳng giới hạn bởi các đường:
y=\(\left|lgX\right|\) , y=0,x=\(\frac{1}{10}\), x=10
Theo dõi (0) 1 Trả lời -


Tính diện tích hình phẳng (H) giới hạn bởi y=sin2x.cos3x, y=0, x=0, x=pi/2
bởi thu thủy
 27/09/2018
27/09/2018
Tính diện tích hình phẳng (H) y=sin2x.cos3x , y=0 ,x=0 , x=pi/2
Theo dõi (0) 1 Trả lời -


Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số (x-1)/(x+2) và đường y=2, y=-2x-4
bởi Trần Anh
 26/04/2018
26/04/2018
tinh dien tich cua hinh phang duoc gioi han boi do thi ham so (x-1)/(x+2) va duong thang y=2;y=-2x-4
Theo dõi (0) 0 Trả lời -


Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành
bởi Èo Lèo
 26/04/2018
26/04/2018
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số y=căn x , trục hoành và đường thẳng y =x - 2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
Theo dõi (0) 0 Trả lời -


Tính diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số y=2^x-2, y=0 và x=2
bởi TÂN DUY
 17/04/2018
17/04/2018
Tính diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số y=2^x-2, y=0 và x=2
Theo dõi (1) 1 Trả lời





