Bài tập 39 trang 175 SGK Toán 12 NC
Cho hình phẳng A giới hạn bởi các đường \(y = x{e^{\frac{x}{2}}}\) y = 0, x = 0 và x = 1. Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành.
Hướng dẫn giải chi tiết
Ta có: \(V = \pi \int \limits_0^1 {x^2}{e^x}dx\)
\(\left\{ \begin{array}{l}
u = {x^2}\\
dv = {e^x}dx
\end{array} \right. \Rightarrow \left[ \begin{array}{l}
du = 2xdx\\
v = {e^x}
\end{array} \right.\)
\(\begin{array}{l}
V = \pi (\left. {{x^2}{e^x}} \right|_0^1 - 2\int\limits_0^1 {x{e^x}dx} )\\
= \pi (e - 2{I_1})
\end{array}\)
Với \({I_1} = \int\limits_0^1 {x{e^x}dx} \)
Đặt \(\left\{ \begin{array}{l}
u = x\\
dv = {e^x}dx
\end{array} \right. \Rightarrow \left[ \begin{array}{l}
du = dx\\
v = {e^x}
\end{array} \right.\)
Do đó:
\({I_1} = \left. {x{e^x}} \right|_0^1 - \int\limits_0^1 {{e^x}dx} = e - \left. {{e^x}} \right|_0^1 = 1\)
Vậy \(V = \pi \left( {e - 2} \right)\)
-- Mod Toán 12 HỌC247
-


Diện tích S của hình phẳng H bằng?
bởi Phạm Quốc Tín
 11/04/2020
11/04/2020
Câu 26
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Diện tích
Diện tích Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Câu 1A ạ
Câu 1A ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Viết phương trình mặt phẳng (P) biết mp (P) là mặt phẳng trung trực của đoạn AB với A(1; 1; 2) và B(1; −3; 2)
bởi Thuyết Hồ
 08/04/2020
KIỂM TRA 15 PHÚT Viết phương trình mặt phẳng (P), biết: a. Mp (P) là mặt phẳng trung trực của đoạn AB với A(1; 1; 2) và B(1; −3; 2). b. Mp (P) đi qua điểm C(1; 2; −3) và song song với mặt phẳng (Q) có phương trình : x − 2y 3z 1 = 0. c. Mp (P) đi qua điểm D(1; 1; 2) và có cặp vtcp (2; -1, 1) và (2; -1; 3). d. Mp (P) đi qua điểm E(3; 1; 2) và vuông góc với hai mặt phẳng: (R1): 2x y 2z – 10 = 0 và (R2): 3x 2y z 8 = 0. e. Mp (P) đi qua ba điểm A(1; 2; 3), B(3; 5; 4), C(3; 0; 5).Theo dõi (0) 5 Trả lời
08/04/2020
KIỂM TRA 15 PHÚT Viết phương trình mặt phẳng (P), biết: a. Mp (P) là mặt phẳng trung trực của đoạn AB với A(1; 1; 2) và B(1; −3; 2). b. Mp (P) đi qua điểm C(1; 2; −3) và song song với mặt phẳng (Q) có phương trình : x − 2y 3z 1 = 0. c. Mp (P) đi qua điểm D(1; 1; 2) và có cặp vtcp (2; -1, 1) và (2; -1; 3). d. Mp (P) đi qua điểm E(3; 1; 2) và vuông góc với hai mặt phẳng: (R1): 2x y 2z – 10 = 0 và (R2): 3x 2y z 8 = 0. e. Mp (P) đi qua ba điểm A(1; 2; 3), B(3; 5; 4), C(3; 0; 5).Theo dõi (0) 5 Trả lời -


Tính nguyên hàm cos x/(1-(sinx)^2
bởi Thành Vinh Bùi
 31/03/2020
Tính nguyên hàm
31/03/2020
Tính nguyên hàm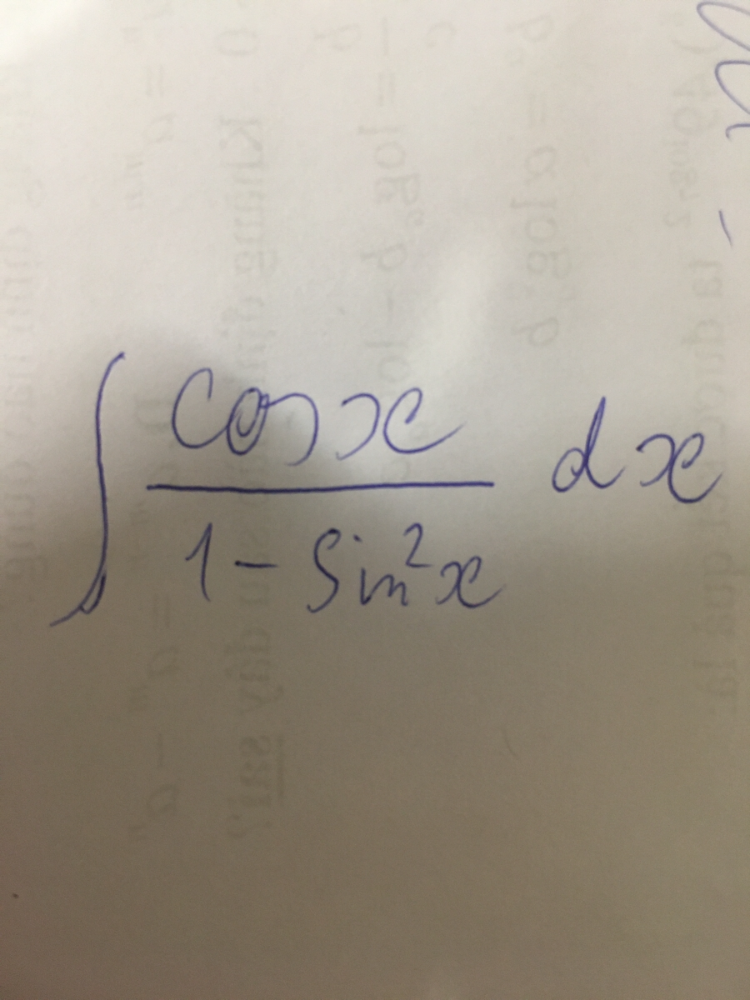 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=ax^3, trục tung và 2 đường thẳng x=-1, x=k (k>0) bằng 17a/4. Tìm k.
bởi Sơn Nguyễn
 30/03/2020
30/03/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời
Bài tập SGK khác
Bài tập 37 trang 175 SGK Toán 12 NC
Bài tập 38 trang 175 SGK Toán 12 NC
Bài tập 40 trang 175 SGK Toán 12 NC
Bài tập 3.31 trang 178 SBT Toán 12
Bài tập 3.32 trang 178 SBT Toán 12
Bài tập 3.33 trang 178 SBT Toán 12
Bài tập 3.34 trang 178 SBT Toán 12
Bài tập 3.35 trang 178 SBT Toán 12
Bài tập 3.36 trang 179 SBT Toán 12
Bài tập 3.37 trang 179 SBT Toán 12
Bài tập 3.38 trang 179 SBT Toán 12
Bài tập 3.39 trang 180 SBT Toán 12
Bài tập 3.40 trang 180 SBT Toán 12





