Bài tập 38 trang 175 SGK Toán 12 NC
Cho hình phẳng A giới hạn bởi các đường y = cosx,y = 0, x = 0 và x = π/4. Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành.
Hướng dẫn giải chi tiết
\(\begin{array}{*{20}{l}}
\begin{array}{l}
V = \pi \int\limits_0^{\frac{\pi }{4}} {{{\cos }^2}xdx} \\
= \frac{\pi }{2}\int\limits_0^{\frac{\pi }{4}} {\left( {1 + {{\cos }^2}} \right)xdx}
\end{array}\\
\begin{array}{l}
= \left. {\frac{\pi }{2}.\left( {x + \frac{1}{2}\sin 2x} \right)} \right|_0^{\frac{\pi }{4}}\\
= \frac{\pi }{2}\left( {\frac{\pi }{4} + \frac{1}{2}} \right) = \frac{{\pi \left( {\pi + 2} \right)}}{8}
\end{array}
\end{array}\)
-- Mod Toán 12 HỌC247
-


Diện tích phần hình phẳng gạch chéo trong hình vẽ dưới được tính theo công thức nào
bởi Cốt Thiên
 25/04/2020
25/04/2020
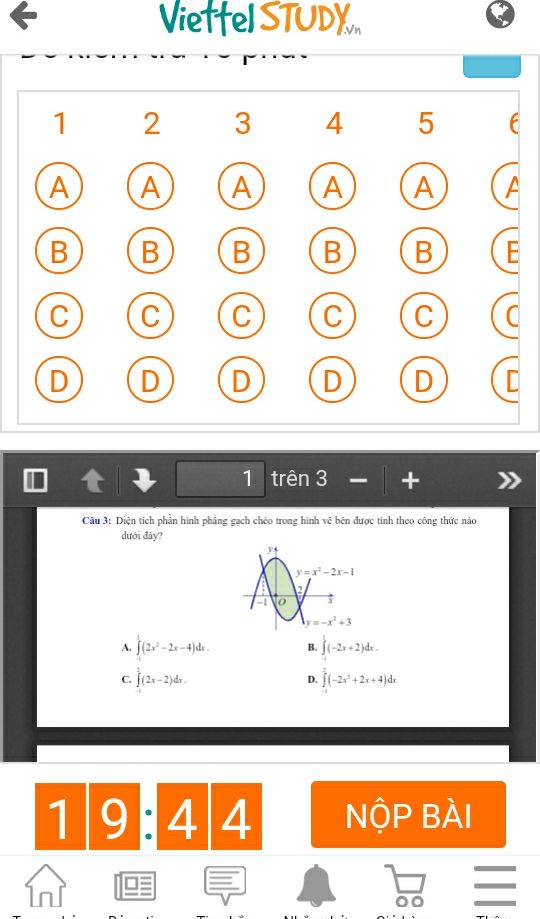 Theo dõi (0) 13 Trả lời
Theo dõi (0) 13 Trả lời -


Tính giá trị \(S = \int\limits_0^1 {{e^x}f(x)dx} + \int\limits_0^1 {{e^x}f'(x)dx} \)?
bởi Minh Trần
 21/04/2020
21/04/2020
Câu 29 nha
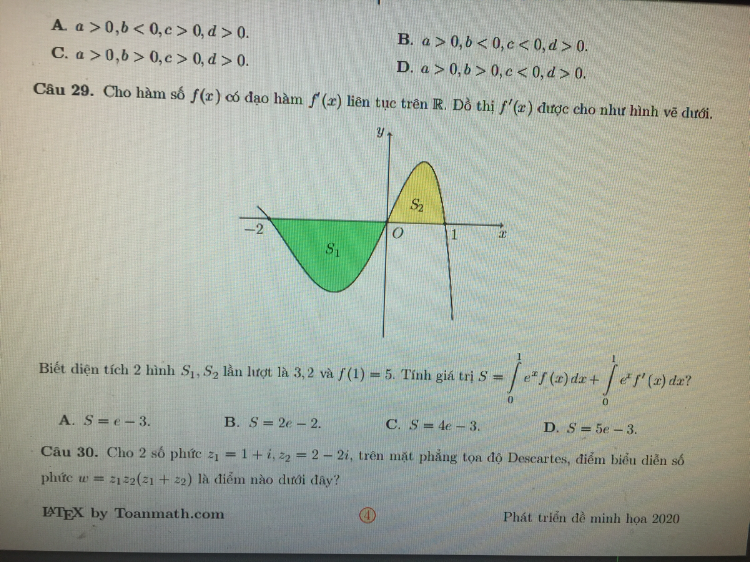 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giá trị dương của tham số m sao cho diện tích hình phẳng giới hạn bởi đồ thị của hàm số y=2x+3 và các đường thẳng y=0,x=0,x=m bằng 10
bởi Mập
 17/04/2020
Theo dõi (0) 0 Trả lời
17/04/2020
Theo dõi (0) 0 Trả lời -


Tính thể tích khối tròn xoay tạo nên khi quay hình phẳng giới hạn bởi các đường y = x^2 - 4, y = 2x - 4 quay quanh trục Ox
bởi Hà Tuấn Anh
 17/04/2020
Tính thể tích khối tròn xoay tạo nên khi quay hình phẳng giới hạn bởi các đường y = x2 - 4, y = 2x - 4 quay quanh trục Ox.Theo dõi (1) 6 Trả lời
17/04/2020
Tính thể tích khối tròn xoay tạo nên khi quay hình phẳng giới hạn bởi các đường y = x2 - 4, y = 2x - 4 quay quanh trục Ox.Theo dõi (1) 6 Trả lời -


Tính thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường sau đây quanh trục Ox?
bởi Hiển Thông
 14/04/2020
14/04/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính diện tích hình phẳng giới hạn bởi các đường sau?
bởi Hiển Thông
 14/04/2020
14/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 36 trang 175 SGK Toán 12 NC
Bài tập 37 trang 175 SGK Toán 12 NC
Bài tập 39 trang 175 SGK Toán 12 NC
Bài tập 40 trang 175 SGK Toán 12 NC
Bài tập 3.31 trang 178 SBT Toán 12
Bài tập 3.32 trang 178 SBT Toán 12
Bài tập 3.33 trang 178 SBT Toán 12
Bài tập 3.34 trang 178 SBT Toán 12
Bài tập 3.35 trang 178 SBT Toán 12
Bài tập 3.36 trang 179 SBT Toán 12
Bài tập 3.37 trang 179 SBT Toán 12
Bài tập 3.38 trang 179 SBT Toán 12
Bài tập 3.39 trang 180 SBT Toán 12
Bài tập 3.40 trang 180 SBT Toán 12





