Giải bài 4 tr 77 sách GK Toán GT lớp 12
Vẽ đồ thị của các hàm số:
a) \(y = logx\).
b) \(y=log_{\frac{1}{2}}x\).
Hướng dẫn giải chi tiết bài 4
Nhận xét:
Mục đích của bài 4 giúp các em ôn lại tính chất và đặc trưng của đồ thị của hàm số lôgarit. Các em chỉ cần thực hiên các bước đơn giản như sau:
Xét hàm số \(y = {\log _a}x(a > 0,a \ne 1)\)
+ Tập xác định: \(D = \left( {0; + \infty } \right)\)
+ Nếu a>1 thì hàm số đồng biến trên \(\left( {0; + \infty } \right)\), nếu 0.
+ Lập bảng giá trị tung độ, hoành đồ các điểm mà đồ thị hàm số đi qua.
+ Vẽ đồ thị.
Lời giải:
Lời giải chi tiết câu a, b bài 4:
Câu a:
Xét hàm số \(y = logx\):
- Tập xác định: \(D = \left( {0; + \infty } \right)\).
- a=10>1 nên hàm số đồng biến trên \(\left( {0; + \infty } \right)\).
- Bảng giá trị:
| x | \(\frac{1}{10}\) | 1 | 10 |
| y | -1 | 0 | 1 |
- Đồ thị hàm số:
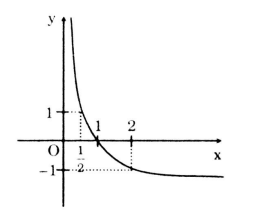
Câu b:
Xét hàm số \(y=log_{\frac{1}{2}}x\)
- Tập xác định: \(D = \left( {0; + \infty } \right)\).
- \(a=\frac{1}{2}<1\) nên hàm số nghịch biến trên \(\left( {0; + \infty } \right)\).
- Bảng giá trị:
| x | \(\frac{1}{2}\) | 1 | 2 |
| y1 | 1 | 0 | -1 |
- Đồ thị hàm số:
-- Mod Toán 12 HỌC247
-


Dùng tính chất đồng biến, nghịch biến của hàm số mũ, hãy so sánh cặp số cho sau: \({\left( {\dfrac{1}{5}} \right)^{\sqrt 2 }}\) và \({\left( {\dfrac{1}{5}} \right)^{1,4}}\)
bởi Tram Anh
 02/10/2022
Theo dõi (0) 1 Trả lời
02/10/2022
Theo dõi (0) 1 Trả lời -


Dùng tính chất đồng biến, nghịch biến của hàm số mũ, hãy so sánh cặp số cho sau: \(\displaystyle {\left( {0,2} \right)^{ - 3}}\) và \(\displaystyle {\left( {0,2} \right)^{ - 2}}\)
bởi Lê Nhật Minh
 03/10/2022
Theo dõi (0) 1 Trả lời
03/10/2022
Theo dõi (0) 1 Trả lời -


Dùng tính chất đồng biến, nghịch biến của hàm số mũ, hãy so sánh cặp số cho sau: \(\displaystyle {\left( {3,2} \right)^{1,5}}\) và \(\displaystyle {\left( {3,2} \right)^{1,6}}\)
bởi Phạm Hoàng Thị Trà Giang
 02/10/2022
Theo dõi (0) 1 Trả lời
02/10/2022
Theo dõi (0) 1 Trả lời -


Dùng tính chất đồng biến, nghịch biến của hàm số mũ, hãy so sánh cặp số cho sau: \(\displaystyle {\left( {0,3} \right)^2}\) và \(1\)
bởi Nguyễn Hoài Thương
 02/10/2022
Theo dõi (0) 1 Trả lời
02/10/2022
Theo dõi (0) 1 Trả lời -


Dùng tính chất đồng biến, nghịch biến của hàm số mũ, hãy so sánh cặp số cho sau: \(\displaystyle {\left( {1,7} \right)^3}\) và \(\displaystyle 1\)
bởi Nhật Mai
 02/10/2022
Theo dõi (0) 1 Trả lời
02/10/2022
Theo dõi (0) 1 Trả lời -


Tìm tọa độ giao điểm của đồ thị của cặp hàm số cho sau: \(y = {\left( {\dfrac{1}{3}} \right)^x}\) và \(\displaystyle y = 9\)
bởi bich thu
 03/10/2022
Theo dõi (0) 1 Trả lời
03/10/2022
Theo dõi (0) 1 Trả lời -


Tìm tọa độ giao điểm của đồ thị của cặp hàm số cho sau: \(y = {\left( {\dfrac{1}{4}} \right)^x}\) và \(y = \dfrac{1}{{16}}\)
bởi con cai
 02/10/2022
Theo dõi (0) 1 Trả lời
02/10/2022
Theo dõi (0) 1 Trả lời -


Tìm tọa độ giao điểm của đồ thị của cặp hàm số cho sau: \(y = {3^x}\) và \(y = \dfrac{1}{3}\)
bởi Phạm Khánh Ngọc
 02/10/2022
Theo dõi (0) 1 Trả lời
02/10/2022
Theo dõi (0) 1 Trả lời -


Tìm tọa độ giao điểm của đồ thị của cặp hàm số cho sau: \(y = {2^x}\) và \(\displaystyle y = 8\)
bởi Nguyễn Xuân Ngạn
 02/10/2022
Theo dõi (0) 1 Trả lời
02/10/2022
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2 trang 77 SGK Giải tích 12
Bài tập 3 trang 77 SGK Giải tích 12
Bài tập 5 trang 78 SGK Giải tích 12
Bài tập 2.27 trang 117 SBT Toán 12
Bài tập 2.28 trang 117 SBT Toán 12
Bài tập 2.29 trang 117 SBT Toán 12
Bài tập 2.30 trang 117 SBT Toán 12
Bài tập 2.31 trang 117 SBT Toán 12
Bài tập 2.32 trang 117 SBT Toán 12
Bài tập 2.33 trang 117 SBT Toán 12
Bài tập 2.34 trang 118 SBT Toán 12
Bài tập 2.35 trang 118 SBT Toán 12
Bài tập 2.36 trang 118 SBT Toán 12
Bài tập 2.37 trang 118 SBT Toán 12
Bài tập 2.38 trang 118 SBT Toán 12
Bài tập 2.39 trang 118 SBT Toán 12
Bài tập 2.40 trang 118 SBT Toán 12
Bài tập 2.41 trang 118 SBT Toán 12
Bài tập 2.42 trang 119 SBT Toán 12
Bài tập 2.43 trang 119 SBT Toán 12
Bài tập 2.44 trang 119 SBT Toán 12
Bài tập 2.45 trang 119 SBT Toán 12
Bài tập 47 trang 111 SGK Toán 12 NC
Bài tập 48 trang 112 SGK Toán 12 NC
Bài tập 49 trang 112 SGK Toán 12 NC
Bài tập 50 trang 112 SGK Toán 12 NC
Bài tập 51 trang 112 SGK Toán 12 NC
Bài tập 52 trang 112 SGK Toán 12 NC
Bài tập 53 trang 113 SGK Toán 12 NC
Bài tập 54 trang 113 SGK Toán 12 NC




.PNG)