Bài tập 49 trang 112 SGK Toán 12 NC
Tính đạo hàm của các hàm số sau:
\(\begin{array}{l}
a)y = \left( {x - 1} \right){e^{2x}}\\
b)y = {x^2}.\sqrt {{e^{4x}} + 1} \\
c)y = \frac{1}{2}\left( {{e^x} - {e^{ - x}}} \right)\\
d)y = \frac{1}{2}({e^x} + {e^{ - x}})
\end{array}\)
Hướng dẫn giải chi tiết
a) \(y\prime = {e^{2x}} + (x - 1).2{e^{2x}} = (2x - 1).{e^{2x}}\)
b)
\(\begin{array}{l}
y' = 2x\sqrt {{e^{4x}} + 1} + {x^2}.\frac{{4{e^{4x}}}}{{2\sqrt {{e^{4x}} + 1} }}\\
= \frac{{2x\left[ {\left( {x + 1} \right){e^{4x}} + 1} \right]}}{{\sqrt {{e^{4x}} + 1} }}
\end{array}\)
c) \(y' = \frac{1}{2}\left( {{e^x} + {e^{ - x}}} \right)\)
d) \(y' = \frac{1}{2}({e^x} - {e^{ - x}})\)
-- Mod Toán 12 HỌC247
-

 2^x 3^x .... 2018^x=2017-x
2^x 3^x .... 2018^x=2017-x Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giá trị lớn nhất của hàm số y=e^x.lnx trên [1;e]?
bởi Thủy Hà
 18/12/2019
Tìm giá trị lớn nhất M của hàm sốTheo dõi (1) 1 Trả lời
18/12/2019
Tìm giá trị lớn nhất M của hàm sốTheo dõi (1) 1 Trả lời -


Phương trình 2^(x+căn(2x+5))-2^(1+căn(2x+5))+2^(6-x)-32=0 có bao nhiêu nghiệm phân biệt?
bởi Hoành Khắc
 17/12/2019
:(
17/12/2019
:( Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


Với hai số thực dương a, b tùy ý và log_3 5.log_5 a/(1+log_3 2)-log_6 b=2, tìm khẳng định đúng?
bởi Trinh Cam
 17/12/2019
.
17/12/2019
. Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Hàm số y =(4x^2-1)^-4 có tập xác định là?
bởi Hoa Nguyen
 15/12/2019
Hàm số y =(4x^2-1)^-4 có tập xác định làTheo dõi (0) 4 Trả lời
15/12/2019
Hàm số y =(4x^2-1)^-4 có tập xác định làTheo dõi (0) 4 Trả lời -


Tìm đạo hàm của hàm số y=2^(x^2)
bởi Sue
 11/12/2019
11/12/2019
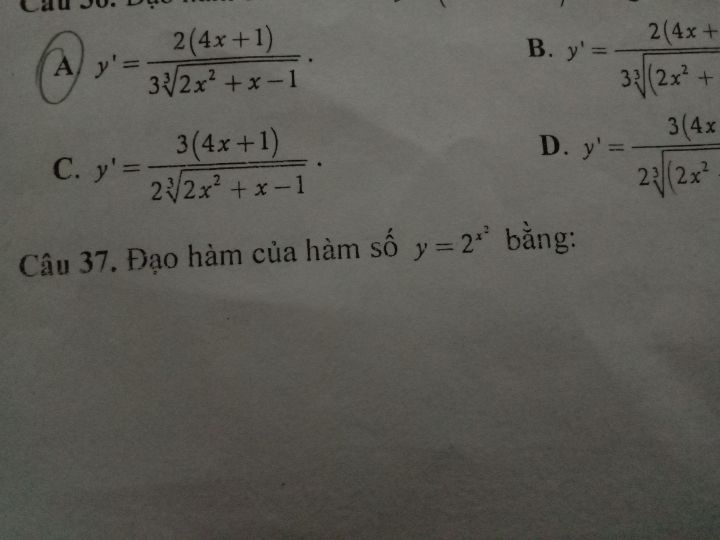 Theo dõi (1) 6 Trả lời
Theo dõi (1) 6 Trả lời -


Tính đạo hàm của x*e^x
bởi Pham Thi Tu Anh
 10/12/2019
Tính đạo hàm của x*e^xTheo dõi (0) 3 Trả lời
10/12/2019
Tính đạo hàm của x*e^xTheo dõi (0) 3 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm tập nghiệm của bất phương trình 5^|2x-2| > 25
bởi Lê Trọng Hiếu
 08/12/2019
Kho Qua
08/12/2019
Kho Qua Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời





