Bài tập 27 trang 90 SGK Toán 12 NC
Hãy tìm lôgarit của mỗi số sau theo cơ số 3:
\(3;81;1;\frac{1}{9};\sqrt[3]{3};\frac{1}{{3\sqrt 3 }}\)
Hướng dẫn giải chi tiết
Áp dụng \({\log _a}{a^b} = b\) với a > 0; a ≠ 1
\(\begin{array}{*{20}{l}}
\begin{array}{l}
{\log _3}3 = 1;{\log _3}81 = {\log _3}{3^4} = 4;\\
{\log _3}1 = 0;{\log _3}\frac{1}{9} = {\log _3}{3^{ - 2}} = - 2;
\end{array}\\
\begin{array}{l}
{\log _3}\sqrt[3]{3} = {\log _3}{3^{\frac{1}{3}}} = \frac{1}{3};\\
{\log _3}\frac{1}{{\sqrt[3]{3}}} = {\log _3}{3^{\frac{{ - 3}}{2}}} = - \frac{3}{2}
\end{array}
\end{array}\)
-- Mod Toán 12 HỌC247
-

 tìm m để 9^x (m-1)×3^x m>0 có nghiệm đúng với mọi x>1Theo dõi (0) 0 Trả lời
tìm m để 9^x (m-1)×3^x m>0 có nghiệm đúng với mọi x>1Theo dõi (0) 0 Trả lời -


Tập nghiệm S của phương trình log3(2x+3)=1
bởi Nguyễn Ngọc Ánh
 20/04/2020
20/04/2020
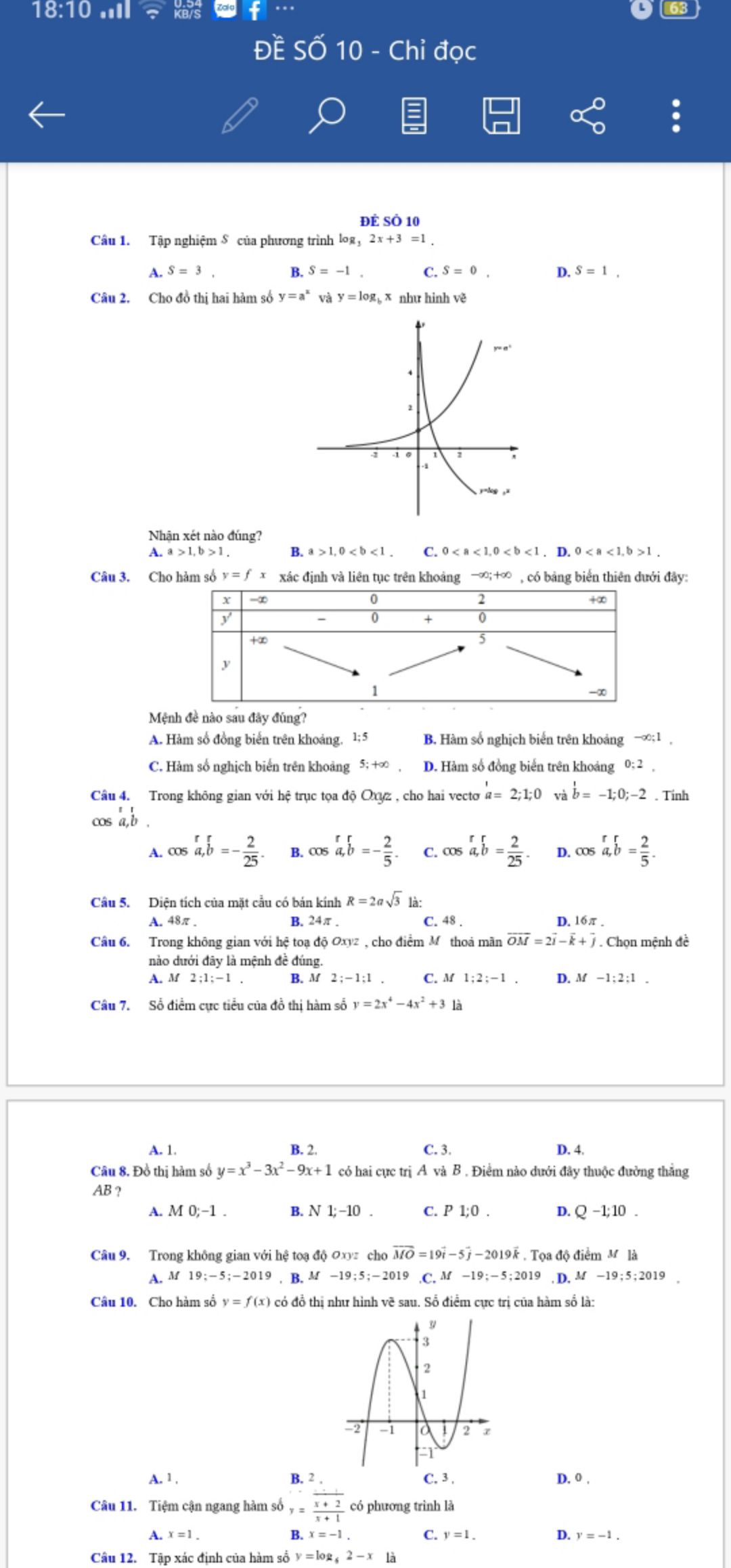 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải phương trình logagit: log3(x^2 - 7) = 2
bởi Lê Chí Tĩnh
 14/04/2020
14/04/2020
Tập nghiệm của phương trình log3(x^2 - 7) = 2
Đáp án A.{-√15;√15} B.{-4;4} C.{4} D.{-4}
Theo dõi (0) 17 Trả lời -


Có taats cả bao nhiêu giá trị nguyên của m để phương trình log 9 x^2 - log 3 (5x-1)=- log 3 m (m là tham số thực).
bởi trà
 02/04/2020
02/04/2020
 Theo dõi (1) 16 Trả lời
Theo dõi (1) 16 Trả lời -


Chọn ngẫu nhiên hai số khác nhau từ 21 số nguyên dương đầu tiên. Tính xác suất để chọn được hai số có tổng là một số chẵn.
bởi Khuất Linh
 25/03/2020
25/03/2020
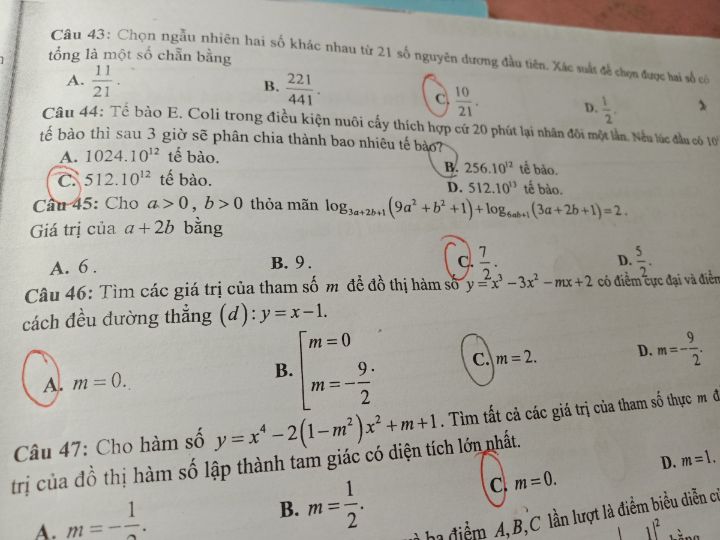 Theo dõi (0) 10 Trả lời
Theo dõi (0) 10 Trả lời -


Tập nghiệm của bát phương trình (ln(x/3))^2<=0
bởi NaNa Minh
 20/03/2020
20/03/2020
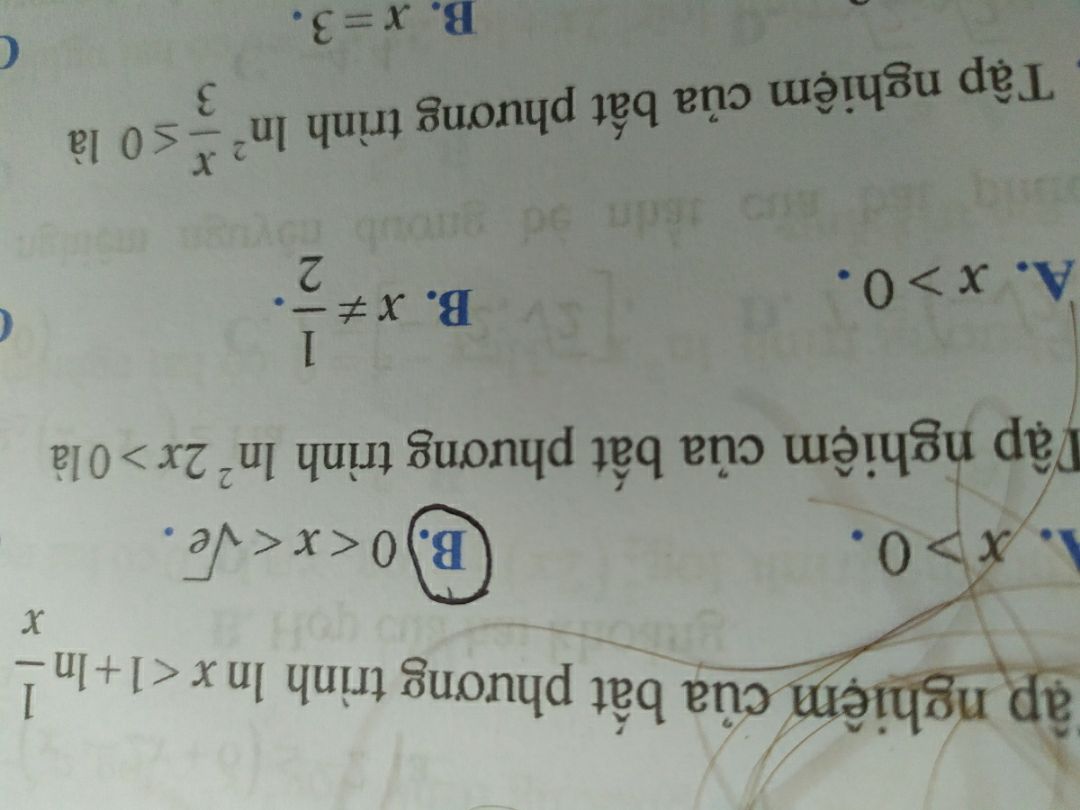 Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


Tìm giá trị lớn nhất và nhỏ nhất của hàm số: f(x)=x^4-2x^2-3 trên đoạn [0;2]?
bởi Nguyen Giang
 20/03/2020
20/03/2020
 Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


Cho phương trình 5x+m = log5(x-m) với m là tham số. Có bao nhiêu giá trị nguyên của m∈(−20;20)m∈(-20;20) để phương trình đã cho có nghiệm?
bởi phạm minh quang
 18/03/2020
Hoặc giúp em giải cây theo hướng tự luận cũng được ai em cám ơn
18/03/2020
Hoặc giúp em giải cây theo hướng tự luận cũng được ai em cám ơn Theo dõi (0) 7 Trả lời
Theo dõi (0) 7 Trả lời -


Tìm tất cả các giá trị của tham số m để phương trình (log3 x)^2+2log3 x -m=0 có nghiệm
bởi Le Anh
 08/03/2020
Giúp mk nhé
08/03/2020
Giúp mk nhé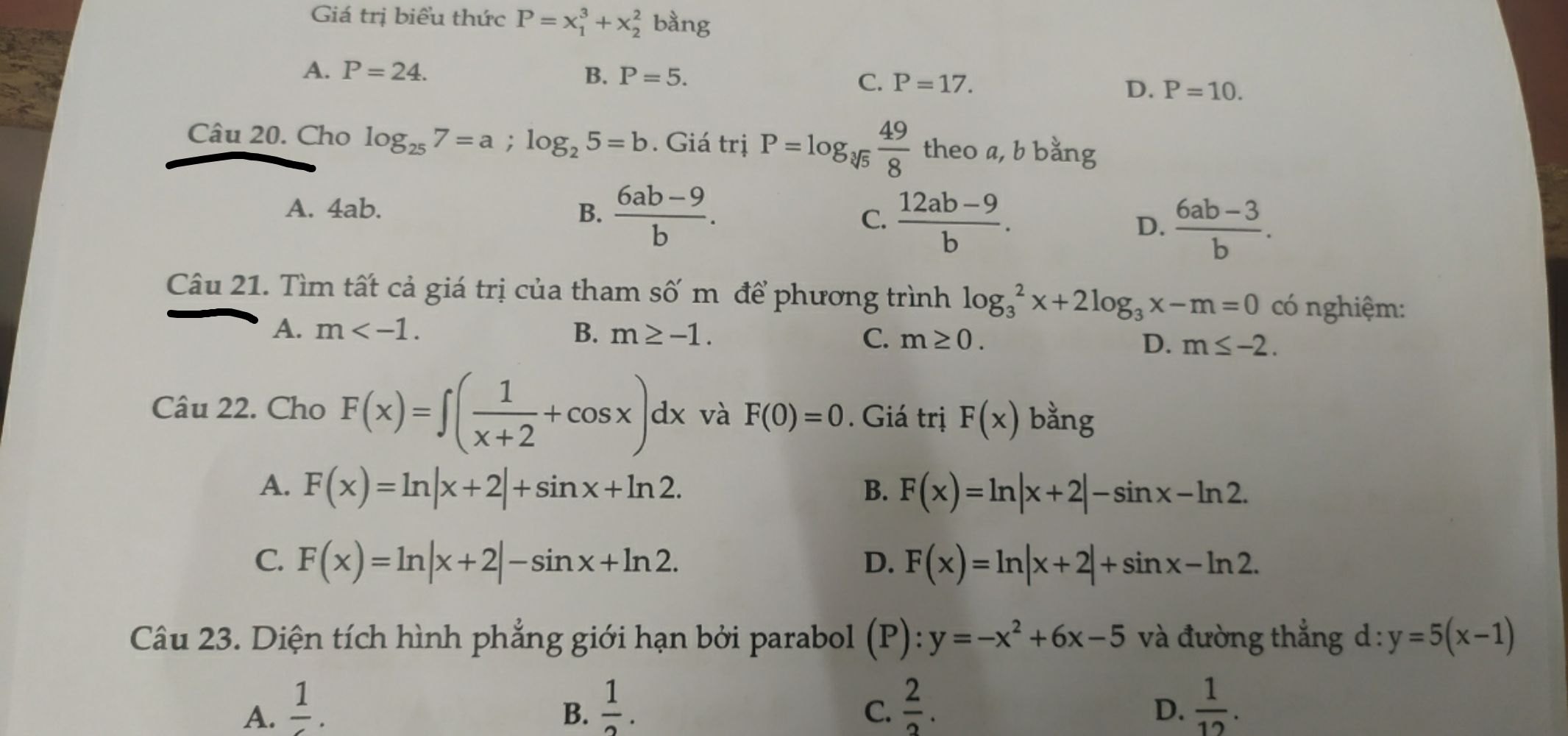 Theo dõi (0) 7 Trả lời
Theo dõi (0) 7 Trả lời -


Có tất cả bao nhiêu giá trị nguyên của m để phương trình (2log_3 ^2 x-log_3x-1).căn(5^x-m)=0 có 2 nghiệm thực phân biệt ?
bởi Nam Trần
 27/02/2020
Help pls !!
27/02/2020
Help pls !! Theo dõi (2) 5 Trả lời
Theo dõi (2) 5 Trả lời
Bài tập SGK khác
Bài tập 25 trang 89 SGK Toán 12 NC
Bài tập 26 trang 89 SGK Toán 12 NC
Bài tập 28 trang 90 SGK Toán 12 NC
Bài tập 29 trang 90 SGK Toán 12 NC
Bài tập 30 trang 90 SGK Toán 12 NC
Bài tập 31 trang 90 SGK Toán 12 NC
Bài tập 32 trang 92 SGK Toán 12 NC
Bài tập 33 trang 92 SGK Toán 12 NC
Bài tập 34 trang 92 SGK Toán 12 NC
Bài tập 35 trang 92 SGK Toán 12 NC
Bài tập 36 trang 93 SGK Toán 12 NC
Bài tập 37 trang 93 SGK Toán 12 NC
Bài tập 38 trang 93 SGK Toán 12 NC
Bài tập 39 trang 93 SGK Toán 12 NC
Bài tập 40 trang 93 SGK Toán 12 NC
Bài tập 41 trang 93 SGK Toán 12 NC
Bài tập 42 trang 97 SGK Toán 12 NC
Bài tập 43 trang 97 SGK Toán 12 NC
Bài tập 44 trang 97 SGK Toán 12 NC





