Bài tập 4 trang 17 SGK Đại số & Giải tích 11

Để vẽ được đồ thị hàm số lượng giác ta cần tìm được chu kì tuần hoàn của hàm số đó:

Trong bài này ta áp dụng nhận xét sau: Hàm số \(y = \sin \left( {ax + b} \right),y = \cos \left( {ax + b} \right)\) với \(a\ne 0\) cho chu kì \(T = \frac{{2\pi }}{{\left| a \right|}}.\).

Lời giải:

Ta có \(sin2(x+k\pi)=sin(2x+2k \pi)=sin2x, k\in \mathbb{Z}\).

Từ đó suy ra hàm số y = sin2x là hàm số tuần hoàn chu kì \(\pi\), mặt khác y = sin2x là hàm số lẻ, do đó ta vẽ đồ thị hàm số y = sin2x trên \(\left [ 0;\frac{\pi }{2} \right ]\), rồi lấy đối xứng qua O ta có đồ thị trên \(\left [ -\frac{\pi }{2};\frac{\pi }{2} \right ]\) rồi sử dụng phép tịnh tiến  \(\vec{v}= (\pi; 0)\) và \(-\vec{v}= (-\pi; 0)\) ta được đồ thị hàm số y = sin2x.

Xét y = sin2x trên \(\left [ 0;\frac{\pi }{2} \right ]\) ta có bảng biến thiên:

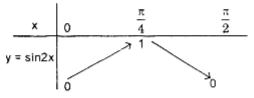
suy ra trên \(\left [ -\frac{\pi }{2};\frac{\pi }{2} \right ]\), y = sin2x có đồ thị dạng:

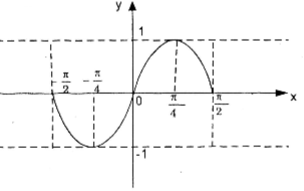
Do vậy đồ thị y = sin2x có dạng:

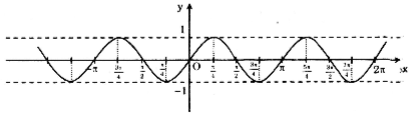
-- Mod Toán 11 HỌC247