Bài tập 3 trang 14 SGK Toán 11 NC
Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi hàm số sau:
a. \(y = 2\cos \left( {x + \frac{\pi }{3}} \right) + 3\)
b. \(y = \sqrt {1 - \sin \left( {{x^2}} \right)} - 1\)
c. \(y = 4\sin \sqrt x \)
Hướng dẫn giải chi tiết
a) Ta có \( - 1 \le \cos \left( {x + \frac{\pi }{3}} \right) \le 1\)
\(\begin{array}{l}
\Rightarrow - 2 \le 2\cos \left( {x + \frac{\pi }{3}} \right) \le 2\\
\Rightarrow 1 \le 2\cos \left( {x + \frac{\pi }{3}} \right) + 3 \le 5\\
\Rightarrow 1 \le y \le 5
\end{array}\)
Vậy \(\min y = 1\) khi \(x + \frac{\pi }{3} = \pi + k2\pi \Leftrightarrow x = \frac{{2\pi }}{3} + k2\pi \) \(k \in Z\)
\(\max y = 5\) khi \(x + \frac{\pi }{3} = k2\pi \Leftrightarrow x = - \frac{\pi }{3} + k2\pi \) \(k \in Z\)
b) Ta có 0 ≤ 1−sinx2 ≤ 2
\(\begin{array}{l}
\Rightarrow - 1 \le \sqrt {1 - \sin \left( {{x^2}} \right)} - 1 \le \sqrt 2 - 1\\
\Rightarrow - 1 \le y \le \sqrt 2 - 1
\end{array}\)
Vậy min y = −1 khi \({x^2} = \frac{\pi }{2} + k2\pi ,k \ge 0,k \in Z\)
\(\max y = \sqrt 2 - 1\) khi \({x^2} = - \frac{\pi }{2} + k2\pi ,k > 0,k \in Z\)
c) Ta có:
\(\begin{array}{l}
- 1 \le \sin \sqrt x \le 1 \Rightarrow - 4 \le 4\sin \sqrt x \le 4\\
\Rightarrow - 4 \le y \le 4
\end{array}\)
Vậy min y = −4 khi \(\sqrt x = - \frac{\pi }{2} + k2\pi ,k > 0,k \in Z\)
max y = 4 khi \(\sqrt x = \frac{\pi }{2} + k2\pi ,k \ge 0,k \in Z\)
-- Mod Toán 11 HỌC247
-


Mong mn giúp em ạ
Theo dõi (0) 0 Trả lời -


Tính đạo hàm của các hàm số sau:
bởi Hậuu Bê
 23/06/2020
23/06/2020
 Theo dõi (3) 0 Trả lời
Theo dõi (3) 0 Trả lời -


Câu 52,53 cách làm trắc nghiệm kiểu j ạ????
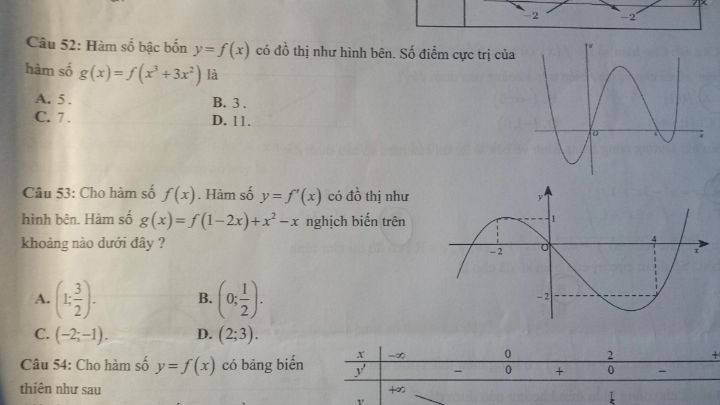 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Hai hàm số nào sau đây có chu kì khác nhau?
bởi Nguyễn Sơn Ca
 28/05/2020
28/05/2020
A. cos(x/2) và sin(x/2).
B. sinx và tanx.
C. cosx và cot(x/2).
D. tan2x và cot2x
Theo dõi (0) 1 Trả lời -


Giá trị nhỏ nhất của hàm số \(y = 3 - 4{\sin ^2}x{\cos ^2}x\) là bao nhiêu?
bởi Lê Bảo An
 29/05/2020
Theo dõi (0) 1 Trả lời
29/05/2020
Theo dõi (0) 1 Trả lời -


Cho hàm số y = (cosx-1)/(cosx+2). Mệnh đề nào trong số các mệnh đề sau đây là sai?
bởi Trần Hoàng Mai
 29/05/2020
29/05/2020
A. Tập xác định của hàm số là ℝ.
B. Hàm số có giá trị lớn nhất bằng 0.
C. Hàm số có giá trị nhỏ nhất bằng - 2.
D. Hàm số tuần hoàn với chu kì T = 2.
Theo dõi (0) 1 Trả lời -


Hàm số y = sinxcos2x là:
bởi Lê Bảo An
 28/05/2020
28/05/2020
A. Hàm chẵn.
B. Hàm không có tính chẵn, lẻ.
C. Hàm không có tính tuần hoàn.
D. Hàm lẻ.
Theo dõi (0) 1 Trả lời -


A. f(x) là hàm số chẵn, g(x) là hàm số lẻ.
B. f(x) là hàm số lẻ, g(x) là hàm số chẵn.
C. f(x) là hàm số chẵn, g(x) là hàm số chẵn.
D. f(x) và g(x) đều là hàm số lẻ.
Theo dõi (0) 1 Trả lời -


Tìm chu kì của hàm số y = cos2x + sin(x/2)
bởi Mai Bảo Khánh
 28/05/2020
Theo dõi (0) 1 Trả lời
28/05/2020
Theo dõi (0) 1 Trả lời -


Tìm tập xác định của hàm số y = 2020/sinx
bởi Trịnh Lan Trinh
 28/05/2020
Theo dõi (0) 1 Trả lời
28/05/2020
Theo dõi (0) 1 Trả lời -


A.T = π. B.T = 2π.
C.T = π2 D.T = π/2.
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1 trang 14 SGK Toán 11 NC
Bài tập 2 trang 14 SGK Toán 11 NC
Bài tập 4 trang 14 SGK Toán 11 NC
Bài tập 5 trang 14 SGK Toán 11 NC
Bài tập 6 trang 15 SGK Toán 11 NC
Bài tập 7 trang 16 SGK Toán 11 NC
Bài tập 8 trang 17 SGK Toán 11 NC
Bài tập 9 trang 17 SGK Toán 11 NC
Bài tập 10 trang 17 SGK Toán 11 NC
Bài tập 11 trang 17 SGK Toán 11 NC






