Bài tập 10 trang 17 SGK Toán 11 NC
Chứng minh rằng mọi giao điểm của đường thẳng xác định bởi phương trình \(y = \frac{x}{3}\) với đồ thị của hàm số y = sinx đều cách gốc tọa độ một khoảng nhỏ hơn \(\sqrt {10} \).
Hướng dẫn giải chi tiết
Đường thẳng \(y = \frac{x}{3}\) đi qua các điểm E(−3;−1) và F(3;1)
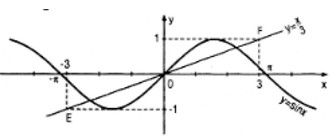
Chỉ có đoạn thẳng EF của đường thẳng đó nằm trong dải {(x;y)|−1 ≤ y ≤ 1} (dải này chứa đồ thị của hàm số y = sinx). Vậy các giao điểm của đường thẳng \(y = \frac{x}{3}\) với đồ thị của hàm số y = sinx phải thuộc đoạn EF; mọi điểm của đoạn thẳng này cách O một khoảng dài hơn \(\sqrt {9 + 1} = \sqrt {10} \) (và rõ ràng E, F không thuộc đồ thị của hàm số y = sinx).
-- Mod Toán 11 HỌC247
-
Tìm tập xác định :
\(y=\frac{\sqrt{1-sinx}}{tanx\left(cosx-1\right)}\)
Theo dõi (0) 1 Trả lời -
Xét tính chẵn lẻ của hàm số y=-3cosx + 2
bởi Nguyễn Trà Giang
25/09/2018
Xét tính chẵn lẻ của hàm số :
y= -3cosx + 2
Theo dõi (0) 1 Trả lời -
Tìm GTLN, GTNN của hàm số y= 2sin4x+3
bởi Lê Tường Vy
25/09/2018
tìm GTLN,GTNN của hàm số
y= 2sin4x+3
Theo dõi (0) 1 Trả lời -
Tìm GTLN, GTNN của hàm số y=3cosx +1
bởi Nguyễn Phương Khanh
25/09/2018
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số
y= 3cosx +1
Theo dõi (0) 1 Trả lời -
tìm tập xác định của hàm số
y=\(\frac{\sqrt{1+cos3x}}{sin2x\left(1-cos4x\right)}\)
y= (1+tanx)2-\(\frac{5cosx}{tanxcos2x}\)
Theo dõi (0) 1 Trả lời -
Tìm tập xác định hàm số y=căn (cos5x +1)
bởi Sam sung
25/09/2018
Tìm tập xác định hàm số
y=căn cos5x +1
Theo dõi (0) 1 Trả lời -
Tìm GTLN, GTNN của y=sin^4 x-cos^4 x
bởi Lê Ngọc
13/06/2018
Tìm giá trị lớn nhất, nhỏ nhất:
a) y= sin^4 x - Cos^4 x
b) y= 1/ Cosx + 1
Theo dõi (0) 1 Trả lời -
Chứng minh y+y^n-4cosx=0 biết y=(2x+1)sinx
bởi hoàng Hương
20/04/2018
cứu e với ạ!!!!
cho hàm số y=(2x+1)sinx. Chứng minh rằng :y + y^n - 4cosx=0.
Theo dõi (0) 0 Trả lời -
Phương trình 1+cosx=m có đúng 2 nghiệm x thuộc (pi/2, 3pi/2) khi và chỉ khi ?
bởi Nguyễn Thiện
08/10/2017
phương trình 1+cosx=m có đúng 2 nghiệm x\(\epsilon\) ( \(\pi\)/2 ; 3\(\pi\)/2) khi và chỉ khi
Theo dõi (0) 9 Trả lời -
Gíá trị lớn nhất, nhỏ nhất của hàm số
bởi Tran Sa
16/09/2017
Hàm số y= \(sin^{2}x + 2\) có GTLN, GTNN là?
Theo dõi (0) 2 Trả lời -
Gíá trị lớn nhất, nhỏ nhất của hàm số
bởi Tran Sa
16/09/2017
Hàm số y=sinx + cosx có GTLN và GTNN là?
Theo dõi (0) 1 Trả lời -
Tìm GTNN của y=2cos2x+2sin2x trên R
bởi nguyen thi quynh
16/08/2017
tim gi tri nho nhat lon nhat
a, y=2cos2x+2sin2xtren r
b, y=can3cos3x-sin3x tren r
c. y=sinx+cosx-sinx*cosxtren r
Theo dõi (0) 1 Trả lời
