Phß║¦n hŲ░ß╗øng dß║½n giß║Żi b├Āi tß║Łp To├Īn 10 ChŲ░ŲĪng 3 B├Āi 2 PhŲ░ŲĪng tr├¼nh quy vß╗ü phŲ░ŲĪng tr├¼nh bß║Łc nhß║źt, bß║Łc hai sß║Į gi├║p c├Īc em nß║»m ─æŲ░ß╗Żc phŲ░ŲĪng ph├Īp v├Ā r├©n luyß╗ćn k─® n─āng c├Īc giß║Żi b├Āi tß║Łp tß╗½ SGK ─Éß║Īi sß╗æ 10 CŲĪ bß║Żn v├Ā N├óng cao.
-
B├Āi tß║Łp 1 trang 62 SGK ─Éß║Īi sß╗æ 10
Giß║Żi c├Īc phŲ░ŲĪng tr├¼nh
a) \(\frac{x^{2}+3x+2}{2x +3}=\) \(\frac{2x -5}{4}\);
b) \(\frac{2x +3}{x - 3}-\frac{4}{x+3}=\frac{24}{x^{2}-9} + 2\) ;
c) \(\sqrt{3x - 5}= 3\) ;
d) \(\sqrt{2x + 5}= 2\) .
-
B├Āi tß║Łp 2 trang 62 SGK ─Éß║Īi sß╗æ 10
Giß║Żi v├Ā biß╗ćn luß║Łn c├Īc phŲ░ŲĪng tr├¼nh sau theo tham sß╗æ m
a) \(m(x - 2) = 3x + 1\);
b) \(m^2x + 6 = 4x + 3m\);
c) \((2m + 1)x - 2m = 3x - 2\).
-
B├Āi tß║Łp 3 trang 62 SGK ─Éß║Īi sß╗æ 10
C├│ hai rß╗Ģ qu├Įt chß╗®a sß╗æ qu├Įt bß║▒ng nhau. Nß║┐u lß║źy 30 quß║Ż ß╗¤ rß╗Ģ thß╗® nhß║źt ─æŲ░a sang rß╗Ģ thß╗® hai th├¼ sß╗æ quß║Ż ß╗¤ rß╗Ģ thß╗® hai bß║▒ng
cß╗¦a b├¼nh phŲ░ŲĪng sß╗æ quß║Ż c├▓n lß║Īi ß╗¤ rß╗Ģ thß╗® nhß║źt. Hß╗Åi sß╗æ quß║Ż qu├Įt ß╗¤ mß╗Śi rß╗Ģ l├║c ban ─æß║¦u l├Ā bao nhi├¬u ?
-
B├Āi tß║Łp 4 trang 62 SGK ─Éß║Īi sß╗æ 10
Giß║Żi c├Īc phŲ░ŲĪng tr├¼nh
a) \(2x^4 -7x^2 + 5 = 0\);
b) \(3x^4 + 2x^2 - 1 = 0\).
-
B├Āi tß║Łp 5 trang 62 SGK ─Éß║Īi sß╗æ 10
Giß║Żi c├Īc phŲ░ŲĪng tr├¼nh sau bß║▒ng m├Īy t├Łnh bß╗Å t├║i (l├Ām tr├▓n kß║┐t quß║Ż ─æß║┐n chß╗» sß╗æ thß║Łp ph├ón thß╗® ba)
a) \(2x^2 - 5x + 4 = 0\);
b) \(-3x^2 + 4x + 2 = 0\);
c) \(3x^2 + 7x + 4 = 0\);
d) \(9x^2 - 6x - 4 = 0\).
-
B├Āi tß║Łp 6 trang 62 SGK ─Éß║Īi sß╗æ 10
Giß║Żi c├Īc phŲ░ŲĪng tr├¼nh.
a) \(|3x - 2| = 2x + 3\);
b) \(|2x -1| = |-5x - 2|\);
c) \(\frac{x-1}{2x -3}=\frac{-3x+1}{|x+1|};\)
d) \(|2x + 5| = x^2 +5x +1.\)
-
B├Āi tß║Łp 7 trang 62 SGK ─Éß║Īi sß╗æ 10
Giß║Żi c├Īc phŲ░ŲĪng tr├¼nh
a) \(\sqrt{5x +6} = x - 6;\)
b) \(\sqrt{3 -x}=\sqrt{x +2}+1;\)
c) \(\sqrt{2x^{2} +5}= x + 2.\)
d) \(\sqrt{4x^{2} +2x + 10} = 3x + 1.\)
-
B├Āi tß║Łp 8 trang 62 SGK ─Éß║Īi sß╗æ 10
Cho phŲ░ŲĪng tr├¼nh \(3x^2 - 2(m + 1)x + 3m - 5 = 0.\)
X├Īc ─æß╗ŗnh m ─æß╗ā phŲ░ŲĪng tr├¼nh c├│ mß╗Öt nghiß╗ćm gß║źp ba nghiß╗ćm kia. T├Łnh c├Īc nghiß╗ćm trong trŲ░ß╗Øng hß╗Żp ─æ├│.
-
B├Āi tß║Łp 3.13 trang 66 SGK To├Īn 10
Giß║Żi v├Ā biß╗ćn luß║Łn theo tham sß╗æ m c├Īc phŲ░ŲĪng tr├¼nh sau:
a) \(m\left( {m - 6} \right)x + m = - 8x + {m^2} - 2\)
b) \(\frac{{\left( {m - 2} \right)x + 3}}{{x + 1}} = 2m - 1\)
c) \(\frac{{\left( {2m + 1} \right)x - m}}{{x - 1}} = x + m\)
d) \(\frac{{\left( {3m - 2} \right)x - 5}}{{x - m}} = - 3\)
-
B├Āi tß║Łp 3.14 trang 55 SBT To├Īn 10
Cho phŲ░ŲĪng tr├¼nh
(m + 2)x2 + (2m + 1)x + 2 = 0
a) X├Īc ─æß╗ŗnh m ─æß╗ā phŲ░ŲĪng tr├¼nh c├│ hai nghiß╗ćm tr├Īi dß║źu v├Ā tß╗Ģng hai nghiß╗ćm bß║▒ng -3.
b) Vß╗øi gi├Ī trß╗ŗ n├Āo cß╗¦a m th├¼ phŲ░ŲĪng tr├¼nh c├│ nghiß╗ćm k├®p? T├¼m nghiß╗ćm k├®p ─æ├│.
-
B├Āi tß║Łp 3.15 trang 66 SBT To├Īn 10
Cho phŲ░ŲĪng tr├¼nh 9x2 + 2(m2 - 1)x + 1 = 0
a) Chß╗®ng tß╗Å rß║▒ng vß╗øi m > 2 phŲ░ŲĪng tr├¼nh c├│ hai nghiß╗ćm ph├ón biß╗ćt ├óm.
b) X├Īc ─æß╗ŗnh m ─æß╗ā phŲ░ŲĪng tr├¼nh c├│ hai nghiß╗ćm x1, x2 m├Ā x1 + x2 = -4
-
B├Āi tß║Łp 3.16 trang 66 SBT To├Īn 10
Giß║Żi c├Īc phŲ░ŲĪng tr├¼nh:
a) \(\sqrt {3x - 4} = x - 3\)
b) \(\sqrt {{x^2} - 2x + 3} = 2x - 1\)
c) \(\sqrt {2{x^2} + 3x + 7} = x + 2\)
d) \(\sqrt {3{x^2} - 4x - 4} = \sqrt {2x +5} \)
-
B├Āi tß║Łp 3.17 trang 67 SBT To├Īn 10
Giß║Żi v├Ā biß╗ćn luß║Łn theo tham sß╗æ m c├Īc phŲ░ŲĪng tr├¼nh sau
a) \(\left| {3x + 2m} \right| = x - m\)
b) \(\left| {2x + m} \right| = \left| {x - 2m + 2} \right|\)
c) \(m{x^2} + \left( {2m - 1} \right)x + m - 2 = 0\)
d) \(\frac{{\sqrt {4x - 2} }}{{2x - 1}} = m - 1\)
-
B├Āi tß║Łp 3.18 trang 67 SBT To├Īn 10
Nghiß╗ćm cß╗¦a phŲ░ŲĪng tr├¼nh sau l├Ā:
\(\frac{{\left| {x + 3} \right|}}{{3x + 1}} = \left| {2x - 1} \right|\)
A. x = \( - \frac{2}{3}\) B. x = 1
B. x = 1 v├Ā x = \( - \frac{2}{3}\) D. x = \( - \frac{1}{3}\)
-
B├Āi tß║Łp 3.19 trang 67 SBT To├Īn 10
Trong c├Īc gi├Ī trß╗ŗ sau ─æ├óy, gi├Ī trß╗ŗ n├Āo l├Ā nghiß╗ćm cß╗¦a phŲ░ŲĪng tr├¼nh |3x - 4| = x2 + x - 7
A. x = 0 v├Ā x = -2 B. x = 0
C. x = 3 D. x = -2
-
B├Āi tß║Łp 3.20 trang 67 SBT To├Īn 10
T├¼m nghiß╗ćm cß╗¦a phŲ░ŲĪng tr├¼nh sau:
\(1 - \sqrt {4x - 3} = \sqrt { - 2x + 1} \)
A. x = \(\frac{1}{2}\) B. x = 1
C. x = 0 D. phŲ░ŲĪng tr├¼nh v├┤ nghiß╗ćm
-
B├Āi tß║Łp 3.21 trang 67 SBT To├Īn 10
T├¼m nghiß╗ćm cß╗¦a phŲ░ŲĪng tr├¼nh sau:
\(\sqrt {{x^2} - 2x + 9} = 2{x^2} - 4x + 3\)
A. x = 0 v├Ā x = 1 B. x = 1 v├Ā x = 2
C. x = 0 v├Ā x = 2 D. x = 0 v├Ā x = 1
-
B├Āi tß║Łp 3.22 trang 67 SBT To├Īn 10
Nghiß╗ćm cß╗¦a phŲ░ŲĪng tr├¼nh |x2 - 3x + 4| = |4 - 5x| l├Ā:
A. x = 0, x = 2, x = 8 v├Ā x = -4
B. x = 0 v├Ā x = 4
C. x = - 2 v├Ā x = 4
D. x = 1 v├Ā x = -4
-
B├Āi tß║Łp 3.23 trang 68 SBT To├Īn 10
PhŲ░ŲĪng tr├¼nh (m + 1)x2 - 3(m - 1)x + 2 = 0 c├│ mß╗Öt nghiß╗ćm gß║źp ─æ├┤i nghiß╗ćm kia th├¼ gi├Ī trß╗ŗ cß╗¦a tham sß╗æ m l├Ā:
A. m = 1 B. m = -1
C. m = 0 hoß║Ęc m = 3 D. m = 2
-
B├Āi tß║Łp 3.24 trang 68 SBT To├Īn 10
PhŲ░ŲĪng tr├¼nh 3x2 + 5x + 2(m + 1) = 0 c├│ hai nghiß╗ćm ├óm ph├ón biß╗ćt khi tham sß╗æ m nß║▒m trong khoß║Żng n├Āo sau ─æ├óy?
A. 0 < m < 1
B. -1 < m < \(\frac{1}{{24}}\)
C. -2 < m < 0
D. -1 < m < 1
-
B├Āi tß║Łp 3.25 trang 68 SBT To├Īn 10
T├¼m m ─æß╗ā phŲ░ŲĪng tr├¼nh x2 + 2(m + 1)x + 2(m + 6) = 0 c├│ hai nghiß╗ćm x1, x2 m├Ā x1 + x2 = 4
A. m = 1
B. m = -3
C. m = -2
D. Kh├┤ng tß╗ōn tß║Īi m
-
B├Āi tß║Łp 5 trang 78 SGK To├Īn 10 NC
Xem c├Īc b├Āi giß║Żi sau ─æ├óy v├Ā cho biß║┐t mß╗Śi b├Āi giß║Żi ─æ├│ ─æ├║ng hay sai? V├¼ sao?
a) \(\frac{{\left( {x - 2} \right)\left( {x - 1} \right)}}{{\sqrt x - 1}} = 0\)
\(\begin{array}{l}
\Leftrightarrow \frac{{x - 2}}{{\sqrt x - 1}}\left( {x - 1} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
\frac{{x - 2}}{{\sqrt x - 1}} = 0\\
x - 1 = 0
\end{array} \right.
\end{array}\)Ta c├│ \(\frac{{x - 2}}{{\sqrt x - 1}} = 0 \Leftrightarrow x = 2\)
\(x - 1 = 0 \Leftrightarrow x = 1\)
Vß║Ły tß║Łp nghiß╗ćm cß╗¦a phŲ░ŲĪng tr├¼nh ─æ├Ż cho l├Ā S = {1, 2}
b) \(\sqrt {{x^2} - 2} = 1 - x \)
\(\Leftrightarrow {x^2} - 2 = {\left( {1 - x} \right)^2}\)
\(\begin{array}{l}
\Leftrightarrow {x^2} - 2 = 1 - 2x + {x^2}\\
\Leftrightarrow 2x = 3 \Leftrightarrow x = \frac{3}{2}
\end{array}\)Vß║Ły phŲ░ŲĪng tr├¼nh c├│ nghiß╗ćm \(x = \frac{3}{2}\)
-
B├Āi tß║Łp 6 trang 78 SGK To├Īn 10 NC
Giß║Żi v├Ā biß╗ćn luß║Łn c├Īc phŲ░ŲĪng tr├¼nh
a) \((m^2+2)x-2m=x-3\)
b) \(m(x-m)=x+m-2\)
c) \(m(x-m+3)=m(x-2)+6\)
d) \(m^2(x-1)+m=x(3m-2)\)
-
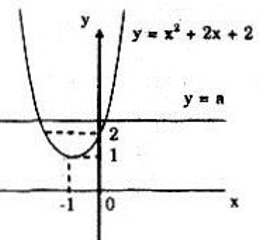
B├Āi tß║Łp 7 trang 78 SGK To├Īn 10 NC
Dß╗▒a v├Āo h├¼nh b├¬n, t├¼m c├Īc gi├Ī trß╗ŗ cß╗¦a a ─æß╗ā phŲ░ŲĪng tr├¼nh: \(3x+2=ŌłÆx^2+x+a\) c├│ nghiß╗ćm dŲ░ŲĪng.
Khi ─æ├│, h├Ży t├¼m nghiß╗ćm dŲ░ŲĪng cß╗¦a phŲ░ŲĪng tr├¼nh.
-
B├Āi tß║Łp 8 trang 78 SGK To├Īn 10 NC
Giß║Żi v├Ā biß╗ćn luß║Łn c├Īc phŲ░ŲĪng tr├¼nh
a) \((m-1)x^2+3x-1=0\)
b) \(x^2-4x+m-3=0\)
-
B├Āi tß║Łp 9 trang 78 SGK To├Īn 10 NC
a) Giß║Ż sß╗Ł phŲ░ŲĪng tr├¼nh ax2 + bx + c = 0 (a ŌēĀ 0) c├│ hai nghiß╗ćm x1 v├Ā x2.
Chß╗®ng minh rß║▒ng: ax2 + bx + c = a(x ŌĆō x1)(x ŌĆō x2)
b) ├üp dß╗źng: Ph├ón t├Łch c├Īc ─æa thß╗®c sau th├Ānh nh├ón tß╗Ł
\(f(x)=-2x^2-7x+4\);
\(g\left( x \right) = \left( {\sqrt 2 + 1} \right){x^2} - 2\left( {\sqrt 2 + 1} \right)x + 2\)
-
B├Āi tß║Łp 10 trang 78 SGK To├Īn 10 NC
Kh├┤ng giß║Żi phŲ░ŲĪng tr├¼nh x2 - 2x - 15 = 0, h├Ży t├Łnh:
a) Tß╗Ģng c├Īc b├¼nh phŲ░ŲĪng hai nghiß╗ćm cß╗¦a n├│.
b) Tß╗Ģng c├Īc lß║Łp phŲ░ŲĪng hai nghiß╗ćm cß╗¦a n├│.
c) Tß╗Ģng c├Īc l┼®y thß╗½a bß║Łc bß╗æn hai nghiß╗ćm cß╗¦a n├│.
HŲ░ß╗øng dß║½n:
\(x_1^4 + x_2^4 = {\left( {x_1^2 + x_2^2} \right)^2} - 2x_1^2x_2^2\)
-
B├Āi tß║Łp 11 trang 79 SGK To├Īn 10 NC
Trong c├Īc khß║│ng ─æß╗ŗnh sau ─æ├óy c├│ duy nhß║źt khß║│ng ─æß╗ŗnh ─æ├║ng. H├Ży chß╗Źn khß║│ng ─æß╗ŗnh ─æ├│. PhŲ░ŲĪng tr├¼nh: \(\left( {\sqrt 3 - 1} \right){x^4} + {x^2} + 2\left( {1 - \sqrt 3 } \right) = 0\).
(A) V├┤ nghiß╗ćm;
(B) C├│ hai nghiß╗ćm \(x = \pm \frac{1}{2}\sqrt {\left( {1 + \sqrt 3 } \right)\left( {\sqrt {33 - 16\sqrt 3 } - 1} \right)} \);
(C) C├│ bß╗æn nghiß╗ćm \(x = \pm \frac{1}{2}\sqrt {\left( {1 + \sqrt 3 } \right)\left( {\sqrt {33 - 16\sqrt 3 } - 1} \right)} \) v├Ā \(x = \pm \sqrt 3 \)
(D) C├│ hai nghiß╗ćm \(x = \pm \sqrt 3 \)
-
B├Āi tß║Łp 12 trang 80 SGK To├Īn 10 NC
Giß║Żi v├Ā biß╗ćn luß║Łn c├Īc phŲ░ŲĪng tr├¼nh sau (m l├Ā tham sß╗æ):
a) 2(m + 1)x - m(x - 1) = 2m + 3;
b) m2(x - 1) + 3mx = (m2 + 3)x - 1;
c) 3(m + 1)x + 4 = 2x + 5(m + 1);
d) m2x + 6 = 4x + 3m.
-
B├Āi tß║Łp 13 trang 80 SGK To├Īn 10 NC
a) T├¼m c├Īc gi├Ī trß╗ŗ cß╗¦a p ─æß╗ā phŲ░ŲĪng tr├¼nh sau v├┤ nghiß╗ćm:
(p + 1)x ŌĆō (x + 2) = 0
b) T├¼m p ─æß╗ā phŲ░ŲĪng tr├¼nh: p2x - p = 4x ŌĆō 2 c├│ v├┤ sß╗æ nghiß╗ćm
-
B├Āi tß║Łp 14 trang 80 SGK To├Īn 10 NC
T├¼m nghiß╗ćm gß║¦n ─æ├║ng cß╗¦a phŲ░ŲĪng tr├¼nh sau ch├Łnh x├Īc ─æß║┐n h├Āng phß║¦n tr─ām.
a) \(x^2-5,6x+6,41=0\);
b) \(\sqrt 2 {x^2} + 4\sqrt 3 x - 2\sqrt 2 = 0\)
-
B├Āi tß║Łp 15 trang 80 SGK To├Īn 10 NC
T├¼m ─æß╗Ö d├Āi c├Īc cß║Īnh cß╗¦a mß╗Öt tam gi├Īc vu├┤ng, biß║┐t rß║▒ng cß║Īnh d├Āi nhß║źt hŲĪn cß║Īnh d├Āi thß╗® hai l├Ā 2m, cß║Īnh d├Āi thß╗® hai hŲĪn cß║Īnh ngß║»n nhß║źt l├Ā 23m.
-
B├Āi tß║Łp 16 trang 80 SGK To├Īn 10 NC
Giß║Żi v├Ā biß╗ćn luß║Łn c├Īc phŲ░ŲĪng tr├¼nh sau (m v├Ā k l├Ā tham sß╗æ),
a) (m - 1)x2 + 7x - 12 = 0;
b) mx2 - 2(m + 3)x + m + 1 = 0;
c) [(k + 1)x - 1](x - 1) = 0;
d) (mx - 2)(2mx - x + 1) = 0.
-
B├Āi tß║Łp 17 trang 80 SGK To├Īn 10 NC
Biß╗ćn luß║Łn sß╗æ giao ─æiß╗ām cß╗¦a hai parabol y = - x2 - 2x + 3 v├Ā y = x2 - m theo tham sß╗æ m.
-
B├Āi tß║Łp 18 trang 80 SGK To├Īn 10 NC
T├¼m c├Īc gi├Ī trß╗ŗ cß╗¦a m ─æß╗ā phŲ░ŲĪng tr├¼nh x2 - 4x + m - 1 = 0 c├│ hai nghiß╗ćm x1 v├Ā x2 thß╗Åa m├Żn hß╗ć thß╗®c x13 + x23 = 40.
-
B├Āi tß║Łp 19 trang 80 SGK To├Īn 10 NC
Giß║Żi phŲ░ŲĪng tr├¼nh x2 + (4m + 1)x + 2(m - 4) = 0, biß║┐t rß║▒ng n├│ c├│ hai nghiß╗ćm v├Ā hiß╗ću giß╗»a nghiß╗ćm lß╗øn v├Ā nghiß╗ćm nhß╗Å bß║▒ng 17.
-
B├Āi tß║Łp 20 trang 81 SGK To├Īn 10 NC
Kh├┤ng giß║Żi phŲ░ŲĪng tr├¼nh, h├Ży x├®t xem mß╗Śi phŲ░ŲĪng tr├¼nh tr├╣ng phŲ░ŲĪng sau c├│ bao nhi├¬u nghiß╗ćm
a) x4 + 8x2 + 12 = 0;
b) -1,5x4 - 2,6x2 + 1 = 0;
c) \(\left( {1 - \sqrt 2 } \right){x^4} + 2{x^2} + 1 - \sqrt 2 = 0\)
d) \( - {x^4} + \left( {\sqrt 3 - \sqrt 2 } \right){x^2} = 0\)
-
B├Āi tß║Łp 21 trang 81 SGK To├Īn 10 NC
Cho phŲ░ŲĪng tr├¼nh: kx2 - 2(k + 1)x + k + 1 = 0.
a) T├¼m k ─æß╗ā phŲ░ŲĪng tr├¼nh tr├¬n c├│ ├Łt nhß║źt mß╗Öt nghiß╗ćm dŲ░ŲĪng.
b) T├¼m c├Īc gi├Ī trß╗ŗ cß╗¦a k ─æß╗ā phŲ░ŲĪng tr├¼nh tr├¬n c├│ mß╗Öt nghiß╗ćm lß╗øn hŲĪn 1 v├Ā mß╗Öt nghiß╗ćm nhß╗Å hŲĪn 1.
(HŲ░ß╗øng dß║½n: ─Éß║Ęt x = y + 1).