Giải bài 3.5 tr 147 SBT Hình học 10
Cho M(1; 2). Hãy lập phương trình của đường thẳng đi qua M và chắn trên hai trục tọa độ hai đoạn có độ dài bằng nhau.
Hướng dẫn giải chi tiết
TH1: \(a \ne 0,b \ne 0\)
Phương trình \(\Delta \) có dạng : \(\frac{x}{a} + \frac{y}{b} = 1\)
Ta có : \(\left| a \right| = \left| b \right|\)
+ b = a
\(\Delta \) có dạng : \(\frac{x}{a} + \frac{y}{a} = 1\)
\(M \in \Delta \Leftrightarrow \frac{1}{a} + \frac{2}{a} = 1 \Leftrightarrow a = 3\)
Vậy \(\Delta :\frac{x}{3} + \frac{y}{3} = 1\) \( \Leftrightarrow x + y - 3 = 0\)
+ b = - a
\(\Delta \) có dạng : \(\frac{x}{a} + \frac{y}{{-a}} = 1\)
\(M \in \Delta \Leftrightarrow \frac{1}{a} + \frac{2}{{ - a}} = 1 \Leftrightarrow a = - 1\)
Vậy \(\Delta :\frac{x}{{ - 1}} + \frac{y}{1} = 1 \Leftrightarrow x - y + 1 = 0\)
TH2: b = a = 0
\(\Delta\) đi qua M và O nên có phương trình là 2x - y = 0
-- Mod Toán 10 HỌC247
-


Tìm góc giữa 2 đường thẳng \(d: 2x-y-10=0\) và \(\Delta: -4x+2y+2002=0\)?
bởi Nguyên Lê Ngọc HuyềnN
 11/06/2020
11/06/2020
Câu 19
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính giá trị của \(\cos \left( {\alpha + \frac{\pi }{3}} \right)\) biết \(\sin \alpha = \frac{1}{{\sqrt 3 }}\) với \(0 < \alpha < \frac{\pi }{2}\)?
bởi An Nguyễn
 10/06/2020
10/06/2020
Các bạn giúp mk với
Bài 38,39
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Ai đó giải chi tiết bài 2 giúp với ạ em cảm ơn rất nhiều ạ
 Theo dõi (2) 0 Trả lời
Theo dõi (2) 0 Trả lời -


Viết phương tình đường trong có tâm là C và tiếp xúc với \(\Delta :\left\{ \begin{array}{l} x = - 3 + 4t\\ y = 2 - 2t \end{array} \right.\)?
bởi linh thục
 10/06/2020
10/06/2020
Giải giúp mình chi tiết bài 1 với. Cảm ơn nhiều
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Tìm tọa độ các điểm M thuộc \(\Delta\) và N thuộc (C) sao cho A là trung điểm của đoạn thẳng MN?
bởi Huệ Hà
 09/06/2020
09/06/2020
Giải giùm mik câu 4 vs
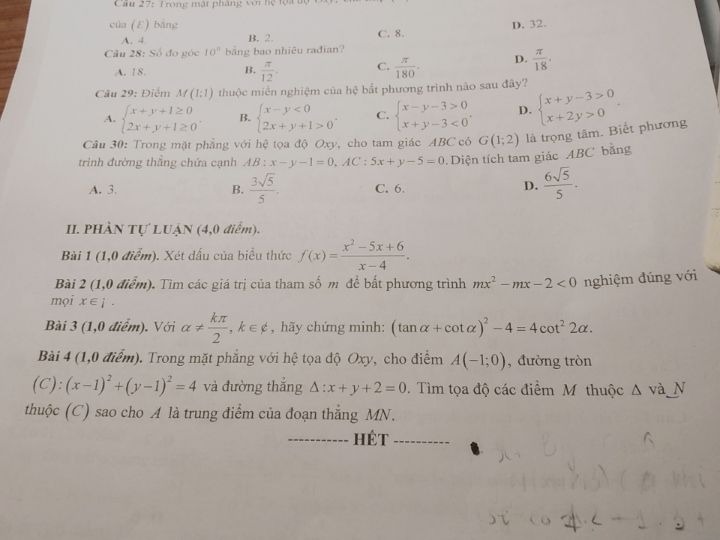 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Viết phương trình tham số của đường trung tuyến CM?
bởi Nas Ks
 09/06/2020
09/06/2020
Giúp mk câu 35,38,40 vs
 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -

Câu 5
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm toạ độ đỉnh C, D, B?
bởi Nguyễn Thị Kim Thu
 08/06/2020
08/06/2020
Trong mặt phẳng oxy, cho hình vuông ABCD có đỉnh A(-1,2). Gọi N là trung điểm CD, đường thẳng BN: 2x y-8=0. Tìm toạ độ đỉnh C, D, B. Biết B có hoành độ lớn hơn 2l
Theo dõi (0) 0 Trả lời -


Viết phương trình d đi qua điểm M (2;7) và cách điểm N (1;2) một khoảng bằng 1?
bởi phung duy nghia
 08/06/2020
08/06/2020
Cần lời giải chi tiết!
Viết phương trình d đi qua điểm M (2;7) và cách điểm N (1;2) một khoảng bằng 1
Theo dõi (1) 1 Trả lời -


Đường thẳng nào đi qua A(2;1) và song song với đường thẳng:2x+3y-2=0?
bởi Nguyễn Thúy Hiền
 08/06/2020
08/06/2020
Câu 8
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời
Bài tập SGK khác
Bài tập 3.3 trang 147 SBT Hình học 10
Bài tập 3.4 trang 147 SBT Hình học 10
Bài tập 3.6 trang 147 SBT Hình học 10
Bài tập 3.7 trang 147 SBT Hình học 10
Bài tập 3.8 trang 147 SBT Hình học 10
Bài tập 3.9 trang 147 SBT Hình học 10
Bài tập 3.10 trang 148 SBT Hình học 10
Bài tập 3.11 trang 148 SBT Hình học 10
Bài tập 3.12 trang 148 SBT Hình học 10
Bài tập 3.13 trang 148 SBT Hình học 10
Bài tập 3.14 trang 148 SBT Hình học 10
Bài tập 1 trang 79 SBT Hình học 10
Bài tập 2 trang 79 SGK Hình học 10 NC
Bài tập 3 trang 80 SGK Hình học 10 NC
Bài tập 4 trang 80 SGK Hình học 10 NC
Bài tập 5 trang 80 SGK Hình học 10 NC
Bài tập 6 trang 80 SGK Hình học 10 NC
Bài tập 7 trang 73 SGK Hình học 10 NC
Bài tập 8 trang 84 SGK Hình học 10 NC
Bài tập 9 trang 84 SGK Hình học 10 NC
Bài tập 10 trang 84 SGK Hình học 10 NC
Bài tập 11 trang 84 SGK Hình học 10 NC
Bài tập 12 trang 84 SGK Hình học 10 NC
Bài tập 13 trang 85 SGK Hình học 10 NC
Bài tập 14 trang 85 SGK Hình học 10 NC
Bài tập 15 trang 89 SGK Hình học 10 NC
Bài tập 16 trang 90 SGK Hình học 10 NC
Bài tập 17 trang 90 SGK Hình học 10 NC
Bài tập 18 trang 90 SGK Hình học 10 NC
Bài tập 19 trang 90 SGK Hình học 10 NC





