Giải bài 3.9 tr 147 SBT Hình học 10
Xét vị trí tương đối của các cặp đường thẳng sau đây:
a) \(d:\left\{ \begin{array}{l}
x = - 1 - 5t\\
y = 2 + 4t
\end{array} \right.\) và \(d':\left\{ \begin{array}{l}
x = - 6 + 5t'\\
y = 2 - 4t'
\end{array} \right.\)
b) \(d:\left\{ \begin{array}{l}
x = 1 - 4t\\
y = 2 + 2t
\end{array} \right.\) và d': 2x + 4y - 10 = 0
c) d: x + y - 2 = 0 và d': 2x + y - 3 = 0
Hướng dẫn giải chi tiết
a) Đưa phương trình của d và d' về dạng tổng quát:
d: 4x + 5y - 6 = 0
d': 4x + 5y + 14 = 0
Ta có : \(\frac{4}{4} = \frac{5}{5} \ne \frac{{ - 6}}{{14}}\)
Vậy d//d'
b) d: x + 2y - 5 = 0
d': 2x + 4y - 10 = 0
Ta có: \(\frac{1}{2} = \frac{2}{4} = \frac{{ - 5}}{{ - 10}}\)
Vậy d ≡ d'
c) d: x + y - 2 = 0
d': 2x + y - 3 = 0
Ta có : \(\frac{1}{2} \ne \frac{1}{1}\)
Vậy d cắt d'
-- Mod Toán 10 HỌC247
-


Tìm điểm M thuộc d có tọa độ nguyên và thỏa mãn khoảng cách từ M đến AB bằng 6
bởi Tuyết Trinh
 27/04/2020
=)))
27/04/2020
=))) Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Tìm điểm đối xứng của N qua đường thẳng (denta)
bởi Thanh Hương
 27/04/2020
27/04/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm B và C biết mặt phẳng tọa độ cho tam giác ABC có A(5;2) đường trung trực cạnh BC có phương trình x+y-6=0
bởi Khải
 27/04/2020
27/04/2020
Trong mặt phẳng tọa độ cho tam giác ABC có A(5;2) đường trung trực cạnh BC có phương trình x y-6=0 và đường trung tuyến CC' là 2x-y 3=0. Tìm B và C
Theo dõi (0) 4 Trả lời -


Viết phương trình tham số của đường thẳng đi qua 2 điểm A(-1;2) và B(-1;-3)
bởi Duy Phuoc
 27/04/2020
27/04/2020
Câu 2(2 điểm). Viết phương trình tham số của đường thẳng đi qua 2 điểm A(-1;2)
và B(-1;-3)?
Câu 3( 2 điểm). Viết phương trình tổng quát của đường thẳng đi qua điểm M(-3;0)
và song song với giá của vectơu (2; 3)
?Câu 4(2 điểm). Viết phương trình tham số của đường thẳng đi qua gốc tọa độ và
vuông góc với đường thẳng 2x +y- 4=0
HếtTheo dõi (0) 1 Trả lời -


Viết phương trình tổng quát của 3 cạnh AB, AC, BC khi biết tọa độ 3 điểm A, B, C
bởi V. Tuấn
 27/04/2020
27/04/2020
 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Viết pt đường thẳng đi qua A và cách B một đoạn bằng 2
bởi Aurora
 26/04/2020
26/04/2020
Cho 3 điểm A(2;0) B(4;1) C(1;2)
a/Viết pt đường thẳng đi qua A và cách B một đoạn bằng 2
b/Viết pt đường phân giác trong của góc A
c/Tính diện tích tam giác ABC
Theo dõi (0) 2 Trả lời -

 Cho hình vuông ABCD tâm I(2;1). M(0;2) thuộc đường AB. N(7/2;-1/2) là trung điểm của CD. Viết phương trình các cạnh của hình vuôngTheo dõi (0) 0 Trả lời
Cho hình vuông ABCD tâm I(2;1). M(0;2) thuộc đường AB. N(7/2;-1/2) là trung điểm của CD. Viết phương trình các cạnh của hình vuôngTheo dõi (0) 0 Trả lời -


Tìm tọa độ đỉnh C biết tam giác ABC có A (2;1), đường cao BH có phương trình x−3y−7=0
bởi Nam Nguyễn
 26/04/2020
26/04/2020
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A (2;1), đường cao BH có phương trình x−3y−7=0 và trung tuyến CM có phương trình x y 1=0x y 1=0. Tìm tọa độ đỉnh C?
Theo dõi (0) 2 Trả lời -


Lập phương trình tham số của đường thẳng AB biết tam giác ABC có A(2; 5), B(1; 1), C(7, 1)
bởi Phu Kiet Pham
 25/04/2020
Cả bài luôn ạ mình cảm ơn nhiều nha
25/04/2020
Cả bài luôn ạ mình cảm ơn nhiều nha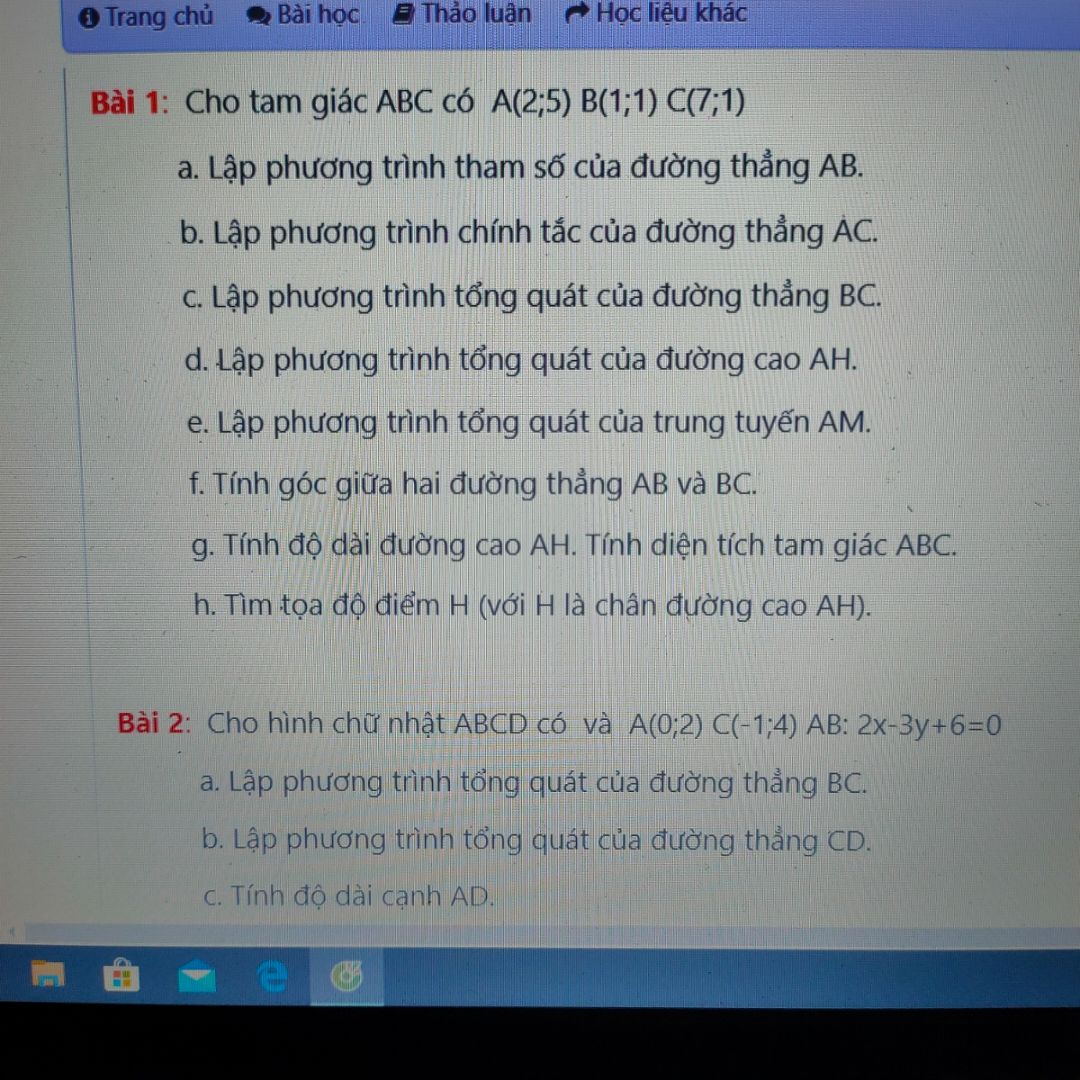 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Viết phương trình cạnh BC?
bởi Aurora
 24/04/2020
24/04/2020
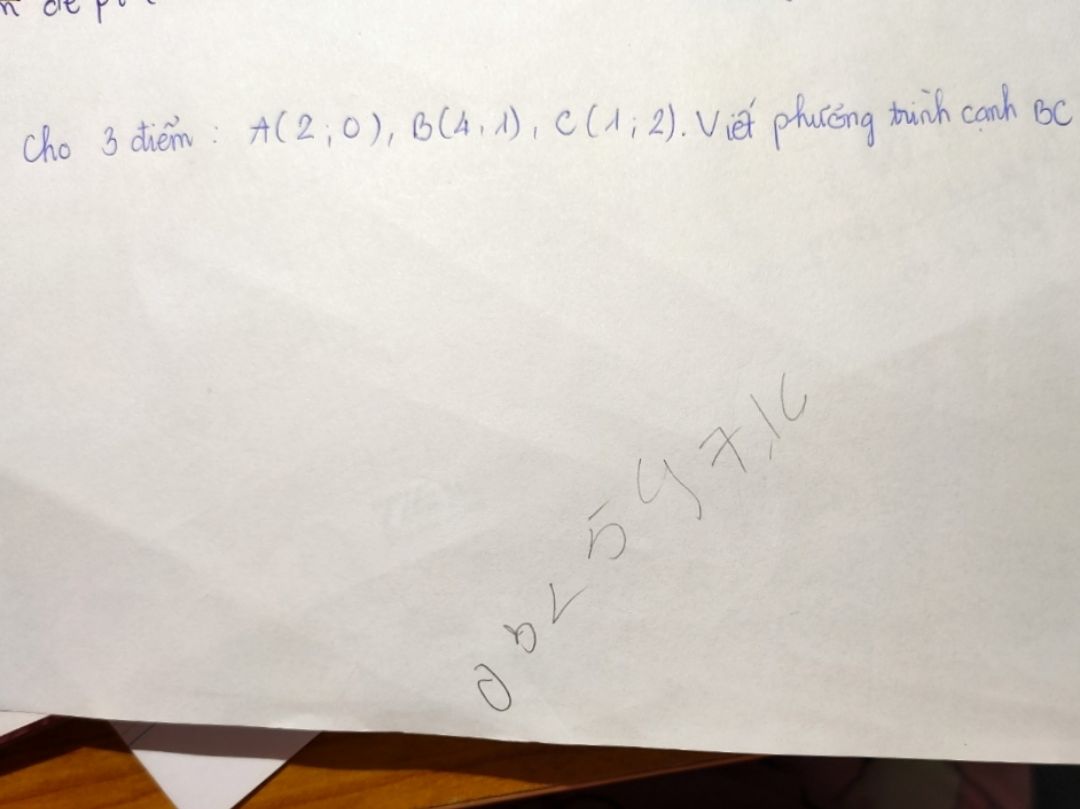 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời
Bài tập SGK khác
Bài tập 3.7 trang 147 SBT Hình học 10
Bài tập 3.8 trang 147 SBT Hình học 10
Bài tập 3.10 trang 148 SBT Hình học 10
Bài tập 3.11 trang 148 SBT Hình học 10
Bài tập 3.12 trang 148 SBT Hình học 10
Bài tập 3.13 trang 148 SBT Hình học 10
Bài tập 3.14 trang 148 SBT Hình học 10
Bài tập 1 trang 79 SBT Hình học 10
Bài tập 2 trang 79 SGK Hình học 10 NC
Bài tập 3 trang 80 SGK Hình học 10 NC
Bài tập 4 trang 80 SGK Hình học 10 NC
Bài tập 5 trang 80 SGK Hình học 10 NC
Bài tập 6 trang 80 SGK Hình học 10 NC
Bài tập 7 trang 73 SGK Hình học 10 NC
Bài tập 8 trang 84 SGK Hình học 10 NC
Bài tập 9 trang 84 SGK Hình học 10 NC
Bài tập 10 trang 84 SGK Hình học 10 NC
Bài tập 11 trang 84 SGK Hình học 10 NC
Bài tập 12 trang 84 SGK Hình học 10 NC
Bài tập 13 trang 85 SGK Hình học 10 NC
Bài tập 14 trang 85 SGK Hình học 10 NC
Bài tập 15 trang 89 SGK Hình học 10 NC
Bài tập 16 trang 90 SGK Hình học 10 NC
Bài tập 17 trang 90 SGK Hình học 10 NC
Bài tập 18 trang 90 SGK Hình học 10 NC
Bài tập 19 trang 90 SGK Hình học 10 NC





