Giải bài 2.38 tr 102 SBT Hình học 10
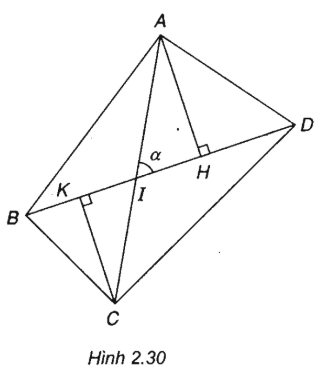
Cho tứ giác lồi ABCD có đường chéo AC = x, đường chéo BD = y và góc tạo bởi AC và BD là α. Gọi S là diện tích của tứ giác ABCD.
a) Chứng minh rằng \(S = \frac{1}{2}xy\sin \alpha \)
b) Nêu kết quả trong trường hợp AC vuông góc với BD.
Hướng dẫn giải chi tiết
a) Ta có: SABCD = SABD + SCBD
Vẽ AH và CK vuông góc với BD.
Gọi I là giao điểm của hai đường chéo AC và BD. Ta có: AH = AI.sinα
\(\begin{array}{l}
{S_{ABCD}} = \frac{1}{2}AH.BD + \frac{1}{2}CK.BD\\
= \frac{1}{2}BD\left( {AH + CK} \right) = \frac{1}{2}BD\left( {AI + IC} \right)\sin \alpha \\
= \frac{1}{2}BD.AC\sin \alpha = \frac{1}{2}xy\sin \alpha
\end{array}\)
b) Nếu AC ⊥ BD thì sinα = 1, khi đó SABCD = \(\frac{{xy}}{2}\). Như vậy nếu tứ giác lồi ABCD có hai đường chéo AC và BD vuông góc với nhau thì diện tích của tứ giác bằng một nửa tích độ dài của hai đường chéo.
-- Mod Toán 10 HỌC247
-


Cạnh nào có độ dài 7.5cm?
bởi Nguyễn Gia Bảo
 02/06/2020
02/06/2020
Tam giác ABC có AB 9cm, AC 12cm, BC 15cm. Khi đó cạnh nào có độ dài 7.5cm?
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABC vuông
bởi Lưu Văn Việt
 22/05/2020
B28 Chứng minh tam giác ABC vuông
22/05/2020
B28 Chứng minh tam giác ABC vuông Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho hình vẽ, độ dài đoạn AC là?
bởi Nga Ngọc
 10/05/2020
10/05/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -

 Hệ lượng giác
Hệ lượng giác Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 2.36 trang 102 SBT Hình học 10
Bài tập 2.37 trang 102 SBT Hình học 10
Bài tập 2.39 trang 102 SBT Hình học 10
Bài tập 2.40 trang 102 SBT Hình học 10
Bài tập 2.41 trang 102 SBT Hình học 10
Bài tập 2.42 trang 102 SBT Hình học 10
Bài tập 2.43 trang 103 SBT Hình học 10
Bài tập 2.44 trang 103 SBT Hình học 10
Bài tập 15 trang 64 SGK Hình học 10 NC
Bài tập 16 trang 64 SGK Hình học 10 NC
Bài tập 17 trang 65 SGK Hình học 10 NC
Bài tập 18 trang 65 SGK Hình học 10 NC
Bài tập 19 trang 65 SGK Hình học 10 NC
Bài tập 20 trang 65 SGK Hình học 10 NC
Bài tập 21 trang 65 SGK Hình học 10 NC
Bài tập 22 trang 65 SGK Hình học 10 NC
Bài tập 23 trang 65 SGK Hình học 10 NC
Bài tập 24 trang 66 SGK Hình học 10 NC
Bài tập 25 trang 66 SGK Hình học 10 NC
Bài tập 26 trang 66 SGK Hình học 10 NC
Bài tập 27 trang 66 SGK Hình học 10 NC
Bài tập 28 trang 66 SGK Hình học 10 NC
Bài tập 29 trang 66 SGK Hình học 10 NC
Bài tập 30 trang 66 SGK Hình học 10 NC
Bài tập 31 trang 66 SGK Hình học 10 NC
Bài tập 32 trang 66 SGK Hình học 10 NC
Bài tập 33 trang 66 SGK Hình học 10 NC
Bài tập 34 trang 66 SGK Hình học 10 NC
Bài tập 35 trang 66 SGK Hình học 10 NC
Bài tập 36 trang 66 SGK Hình học 10 NC