Bài tập 32 trang 66 SGK Hình học 10 NC

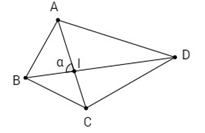
Gọi I là giao điểm của hai đường chéo AC,BD và AIB = α.

Ta có:

\(\begin{array}{l}
{S_{ABI}} = \frac{1}{2}AI.BI\sin \alpha ,\\
{S_{ADI}} = \frac{1}{2}AI.DI\sin \left( {{{180}^0} - \alpha } \right)\\
 = \frac{1}{2}AI.DI\sin \alpha 
\end{array}\)

Suy ra:

\(\begin{array}{l}
{S_{ABD}} = {S_{ABI}} + {S_{ADI}}\\
 = \frac{1}{2}AI\left( {BI + DI} \right)\sin \alpha \\
 = \frac{1}{2}AI.BD.\sin \alpha 
\end{array}\)

Tương tự ta suy ra:

\({S_{BCD}} = {S_{BIC}} + {S_{CDI}} = \frac{1}{2}CI.BD.\sin \alpha \)

Từ đó suy ra: 

\(\begin{array}{l}
{S_{ABCD}} = {S_{ABD}} + {S_{BCD}}\\
 = \frac{1}{2}BD.\left( {AI + CI} \right)\sin \alpha \\
 = \frac{1}{2}BD.AC.\sin \alpha 
\end{array}\)

-- Mod Toán 10 HỌC247