Bài tập 30 trang 66 SGK Hình học 10 NC
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AC và BD. Chứng minh rằng AB2+BC2+CD2+DA2 = AC2+BD2+4MN2.
Hướng dẫn giải chi tiết
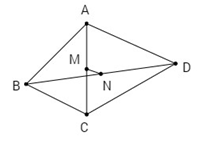
Áp dụng công thức tính trung tuyến, MN là trung tuyến của tam giác BMD, ta có:
\(\begin{array}{l}
M{N^2} = \frac{{B{M^2} + D{M^2}}}{2} - \frac{{B{D^2}}}{4}\\
\Leftrightarrow 4M{N^2} = 2\left( {B{M^2} + D{M^2}} \right) - B{D^2}\left( 1 \right)
\end{array}\)
Tương tự, BM, DM lần lượt là trung tuyến của tam giác ABC, ADC nên:
\(\begin{array}{l}
4B{M^2} = 2\left( {A{B^2} + B{C^2}} \right) - A{C^2}\,\,\,\left( 2 \right)\\
4D{M^2} = 2\left( {D{A^2} + C{D^2}} \right) - A{C^2}\,\,\left( 3 \right)
\end{array}\)
Từ (2), (3) suy ra:
\(\begin{array}{l}
2\left( {B{M^2} + D{M^2}} \right)\\
= A{B^2} + B{C^2} + C{D^2} + D{A^2} - A{C^2}{\mkern 1mu} {\mkern 1mu} \left( 4 \right)
\end{array}\)
Thay (4) vào (1), ta có
4MN2 = AB2+BC2+CD2+DA2−AC2−BD2
⇒ AB2+BC2+CD2+DA2 = AC2+BD2+4MN2
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Bài tập 28 trang 66 SGK Hình học 10 NC
Bài tập 29 trang 66 SGK Hình học 10 NC
Bài tập 31 trang 66 SGK Hình học 10 NC
Bài tập 32 trang 66 SGK Hình học 10 NC
Bài tập 33 trang 66 SGK Hình học 10 NC
Bài tập 34 trang 66 SGK Hình học 10 NC
Bài tập 35 trang 66 SGK Hình học 10 NC
Bài tập 36 trang 66 SGK Hình học 10 NC





